5. Estudio de la estabilidad. Método de Routh
Para que un sistema sea estable la ecuación característica debe cumplir las siguientes premisas:
1. El polinomio en s de la ecuación característica, se escribe ordenado.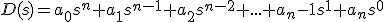
El polinomio debe ser completo (todos los coeficientes tienen que ser distintos de cero, an ≠ 0)
2. Si alguno de los coeficientes es nulo o negativo y hay coeficientes positivos, el sistema no es estable
3. Si todos los coeficientes son positivos, con ellos se construye la tabla de Routh, como se indica. Debe tener tantas filas como el número de términos del polinomio de la función característica, se colocan en filas y columnas como sigue: Las dos primeras filas se van llenando con los coeficientes de los monomios de la ecuación característica, alternando la primera fila con la segunda, y así sucesivamente, hasta que se terminan los coeficientes.
Para calcular coeficientes de las siguientes filas de la tabla, se sigue la siguiente pauta.
Tabla de Routh

Imagen 06. Elaboración propia
De la misma forma, vamos calculando las restantes filas, c, d, e, f,... Hasta completar la tabla.
4. El sistema será estable si en la primera columna de la tabla de Routh no existen cambios de signo.
La condición necesaria para que todas las raíces tengan parte real negativa es:
- Que el polinomio esté completo en s, es decir, que todas las potencias en s, desde sn a so, deben figurar en la ecuación.
- Si algún coeficiente distinto de an, es cero, o si hay algún coeficiente negativo, hay varias raíces positivas o raíces imaginarias con parte real positiva y el sistema es inestable.
Para aclarar lo anterior, vamos a verlo con un ejemplo
La función de transferencia de un sistema de control tiene como expresión:
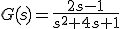
Determinar, aplicando el método de Routh, si el sistema es estable.
Se pueden presentar dos casos especiales:
- Caso 1. Un término de la primera columna, en cualquier fila, es 0 y los demás no.
- Caso 2. Si todos los coeficientes de la fila son cero