En los sistemas de regulación automáticos resulta fundamental conocer la respuesta ante una determinada entrada. Suele ser difícil obtener una relación que permita conocer como va a responder el sistema en función del tiempo ante una entrada determinada, y cuando se conocen estas relaciones, en los regímenes transitorios las relaciones algebraicas (ecuaciones diferenciales) suelen presentar un cálculo muy dificultoso. Para unificar el tratamiento teórico de sistemas tan dispares como pueden ser un vehículo espacial, el control del blanco de una lanzadera de misiles, una central térmica, una tostadora de pan,... se utilizan unas herramientas matemáticas que nos simplifican los cálculos.

Una de esas herramientas consiste en reemplazar funciones de una variable real (tiempo, distancia,..) por otras funciones que dependen de una variable compleja, simplificando ostensiblemente los cálculos. Las operaciones como la integración y la diferenciación se sustituyen por operaciones algebraicas en el plano complejo. Una vez conocido el comportamiento del sistema en el dominio complejo, se puede regresar al dominio del tiempo y de esta manera establecer cuál va a ser la respuesta ante cualquier situación.
Esta técnica se conoce como transformada de LAPLACE, y es una herramienta matemática indispensable en la Regulación Automática.

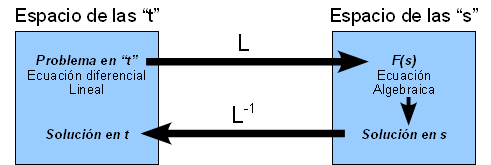Imagen 01. elaboración propia

Definición de la transformada de Laplace de F(t)

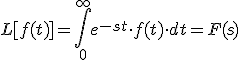
En general F(s) existe siempre que s>α, donde α es un parámetro constante, y donde L es llamado el operador de la transformada de Laplace.
A la función F(s) se le denomina transformada de Laplace de la función f(t). Y simbólicamente se representa así:

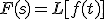
Definición de la transformada inversa de Laplace de F(s)

Si L[f(t)] = F(s), entonces f(t) = L^-1[F(s)] es la transformada inversa de Laplace de F(s). L^-1 se llama operador de la transformada inversa de Laplace.
El cálculo de esta integral es muy laborioso, por lo que se emplean tablas de transformadas y antitransformadas para su resolución.

Los cálculos de hcer la transformada o la transformada inversa, no son sencillos, pero tiene una ventaja muy importante... ¡están ya hechos!.

Veamos una tabla en la que se muestran algunas transformadas (y transformadas inversas) de Laplace:

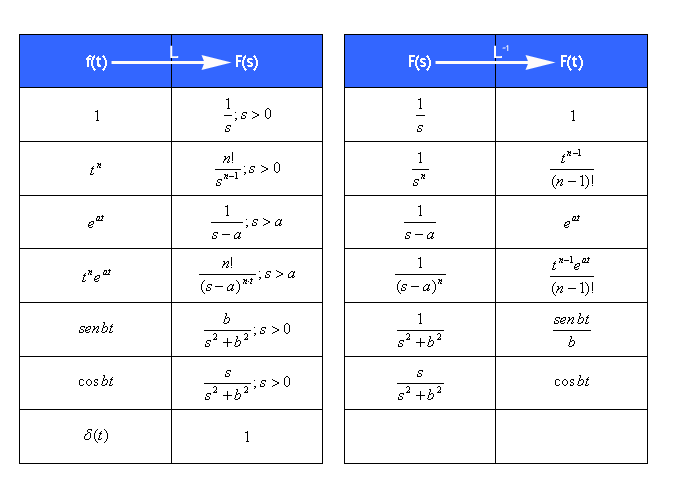Imagen 02. Elaboración propia