7. Simplificación de funciones lógicas

Una vez obtenida la función canónica de una expresión lógica, se debe buscar una expresión simplificada de ésta, con el menor número de términos. Con ello se consigue minimizar el número de errores posibles y abarata su implementación.

Existen dos métodos para conseguir simplificar funciones lógicas.

Icono IDevice Importante

Simplificación por el método algebraico:

Consiste en utilizar todos los postulados, leyes y teoremas enunciados anteriormente.  Con este método se consiguen simplificaciones óptimas, pero hay que tener cierta práctica, no obstante cuando las funciones tienen una expresión grande el procedimiento algebráico puede provocar el que cometamos errores por ser complejo y pesado de utilizar, sobre todo si quien lo realiza no es un experto.

Simplificación por el método de Karnaugh:

Más rápido y eficaz, sobre todo ante problemas complejos.  El método se basa en la construcción de unas tablas con la característica de que entre cada celda y su contigua o adyacente solamente cambia el valor de una variable de entrada.

En este punto vamos a mostrar el funcionamiento del método de Karnaugh. A continuación se adjuntan los mapas de Karnaugh para tres y cuatro variables, indicando en el interior de cada celda a que combinación de variables de entrada corresponde:

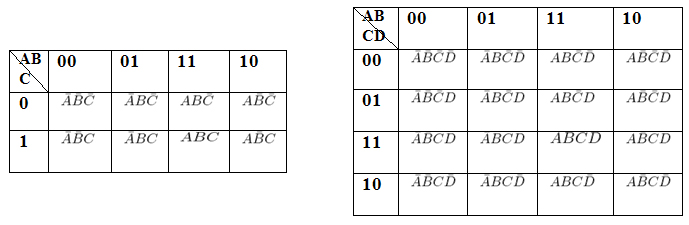Imagen 28. Recurso propio.

Se colocará un 1 en las celdas correspondientes a las combinaciones de las variables de entrada que hacen que la salida sea un 1.

Hay que tener en cuenta que las tablas son contiguas por los flancos extremos, es decir en una tabla de cuatro variables de entrada, las celdas de la columna de la derecha son contiguas a las de la columna de la izquierda, e igualmente ocurre con las casillas de la fila superior y las de la fila inferior.

Imagen 29. Recurso propio.

Es decir se puede considerar que se doblan formando un cilindro, como se observa en la figura anterior, y se vuelve a doblar de nuevo formando un toroide.

Las celdas que ocupan los extremos también son adyacentes, por lo anteriormente descrito.

El método se basa en hacer agrupamientos con el mayor número de celdas posible, siempre que sean potencias de dos (16, 8, 4, 2), tratando que todas las celdas que contengan 1 pertenezcan a agrupaciones de celdas.

Se debe tratar de que no haya celdas comunes a varias agrupaciones, siempre que sea posible. Pero no está prohibido que haya celdas que pertenezcan a más de una agrupación.

Las agrupaciones serán horizontales y verticales; las diagonales no están permitidas.

Aunque si están permitidos las verticales y horizontales que lleguen al final de la fila o la columna, y vuelvan a enlazarse otra vez al inicio, o viceversa.

Se debe procurar que haya el menor número de agrupaciones con el mayor número de unos posible.

La función simplificada tendrá tantos términos como agrupaciones o bolsas tenga el mapa de Karnaugh.

Cada término se obtiene eliminando la o las variables que cambien de estado dentro de la misma bolsa.

  • Una bolsa de 2=21 celdas provoca una simplificación de una variable.
  • Una bolsa de 4=22 celdas provoca una simplificación de dos variables.
  • Una bolsa de 8=23 celdas provoca una simplificación de tres variables.
  • Una bolsa de 16=24 celdas provoca una simplificación de cuatro variables.

Si hubiese una celda aislada que no perteneciese a ninguna agrupación, este término quedaría sin simplificar.

De nuevo vuelve a parecer algo complicado. Veamos algunos ejemplos y lo comprenderás mejor:

« Anterior | Siguiente »