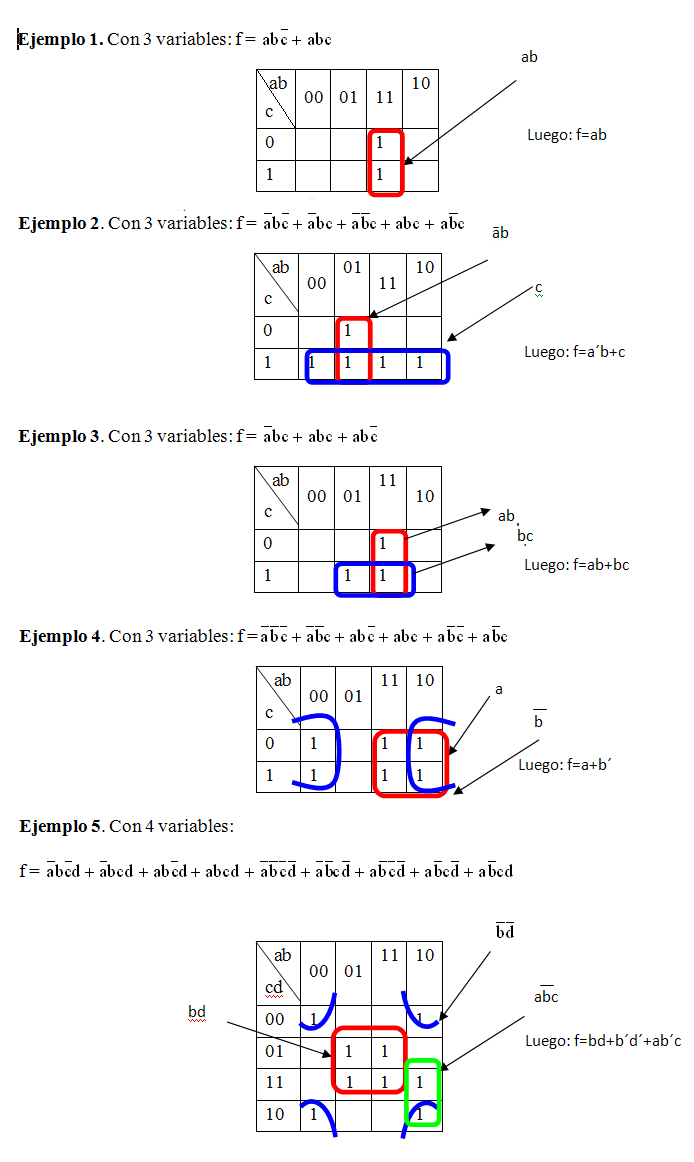
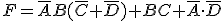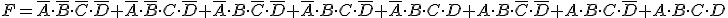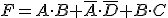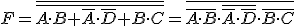Como podemos ver se trata de una función de cuatro variables de entrada, que no está expresada en forma canónica, en primer lugar vamos a obtener su función canónica, en este caso vamos a utilizar el método de la tabla de verdad, para llegar hasta la función canónica:
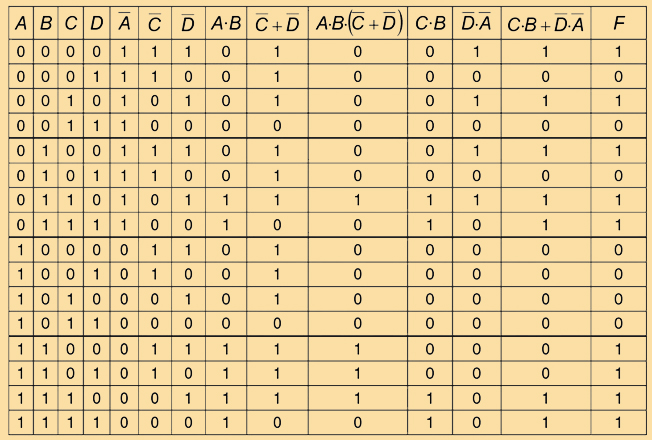 |
Imagen 32. Recurso propio.
|
Tomando las salidas que generan 1, tenemos:
Por lo que al introducir los términos de la función canónica en el mapa de Karnaugh, éste quedará:
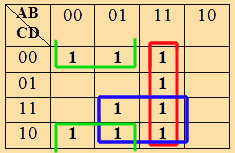 |
Imagen 33. Recurso propio.
|
Se pueden hacer tres bolsas de cuatro celdas cada una, con lo que todas las celdas pertenecerán a alguna agrupación, aunque hay alguna celda que pertenece a más de una bolsa.
La función simplificada constará de tantos términos como bolsas hemos tomado para simplificar (3), de dos variables, ya que las bolsas son de 4=22 celdas cada una. (En cada bolsa desaparecen 2 variables).
Se obtiene la función simplificada:
Que una vez implementada quedaría:
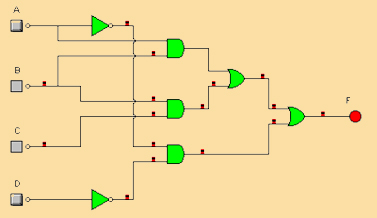 |
Imagen 34. Recurso propio.
|
Para implementarlo empleando únicamente puertas NAND de dos entradas, se debe negar dos veces la función y aplicar el teorema de Morgan a una de las negaciones con lo que se obtiene la expresión:
Que una vez implementada quedará:
 |
Imagen 35. Recurso propio.
|