1. Vueltas y más vueltas
 |
| Imagen de Basilievich con licencia Creative Commons |
Este año, como es tradicional, se ha montado la noria en la feria. La tasa del ayuntamiento por el alquiler de la parcela ha sido de 45.000,00€ para la semana que dura la feria. El gasto en montaje y mantenimiento ha supuesto 6000,00€. El coste para el empresario por realizar un viaje es de 100€.
El coste total según el número de viajes que se dan será:
C(x)=100x+51000
El coste medio por viaje, según el número de viajes que se han dado será:
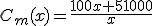
| Nº de Viajes |
50 | 100 | 150 | 200 | 250 | 300 | ... | 1000 |
5000 |
10000 |
15000 |
20000 |
25000 |
30000 |
| Coste medio |
1120,00 | 610,00 |
440,00 | 355,00 |
304,00 | 270,00 |
... | 151,00 |
110,20 |
105,10 |
103,40 |
102,55 |
102,04 |
101,70 |
Está claro que cuantos más viajes demos más nos acercaremos a la cantidad de 100,00 € por coste medio del viaje, pero nunca llegaremos a alcanzarlo. Expresado en términos matemáticos:
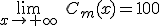
En este caso la recta y=100 es una asíntota horizontal, pues cuanto más viajes damos más se aproxima la función a la recta.
Puedes comprobarlo en la siguiente animación, moviendo el deslizador a valores más grandes y viendo que la diferencia entre la función y la recta y=100 es cada vez más pequeña.
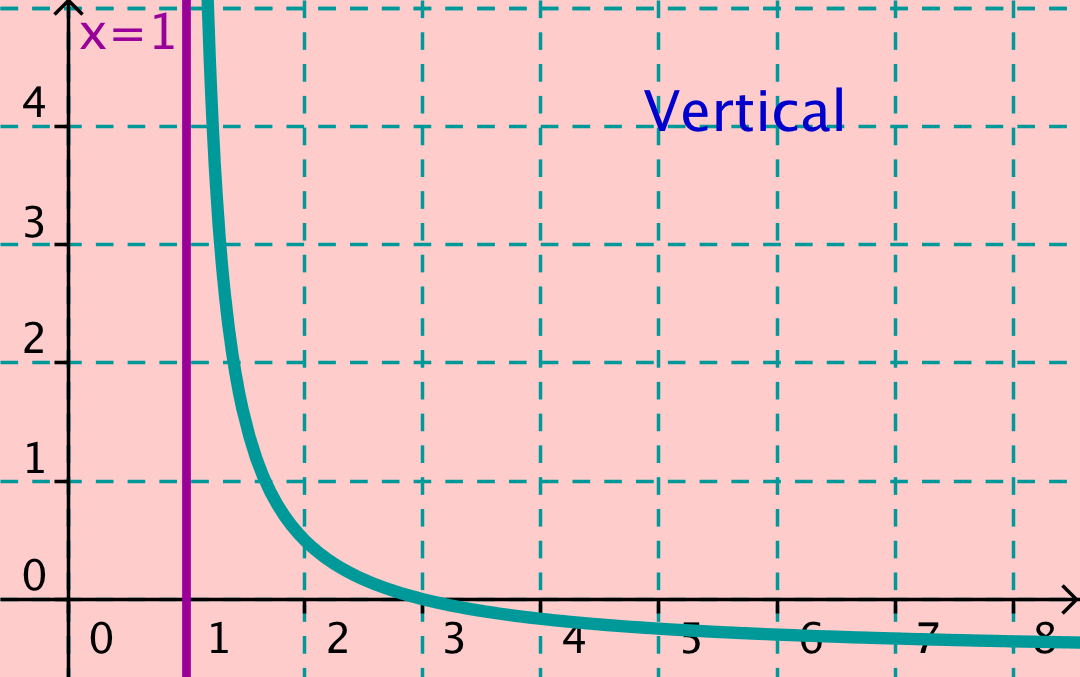
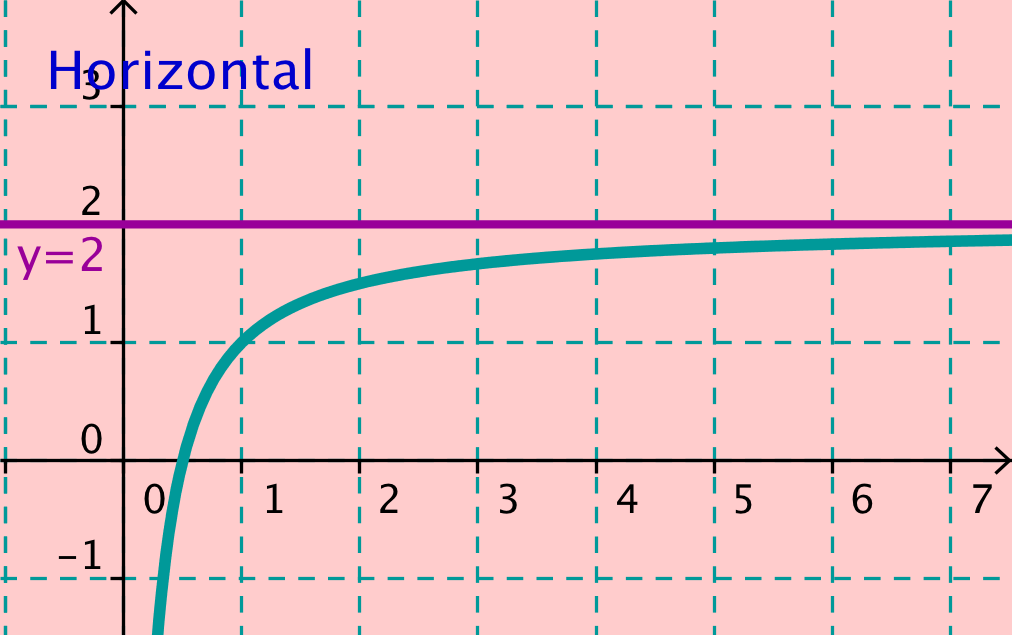
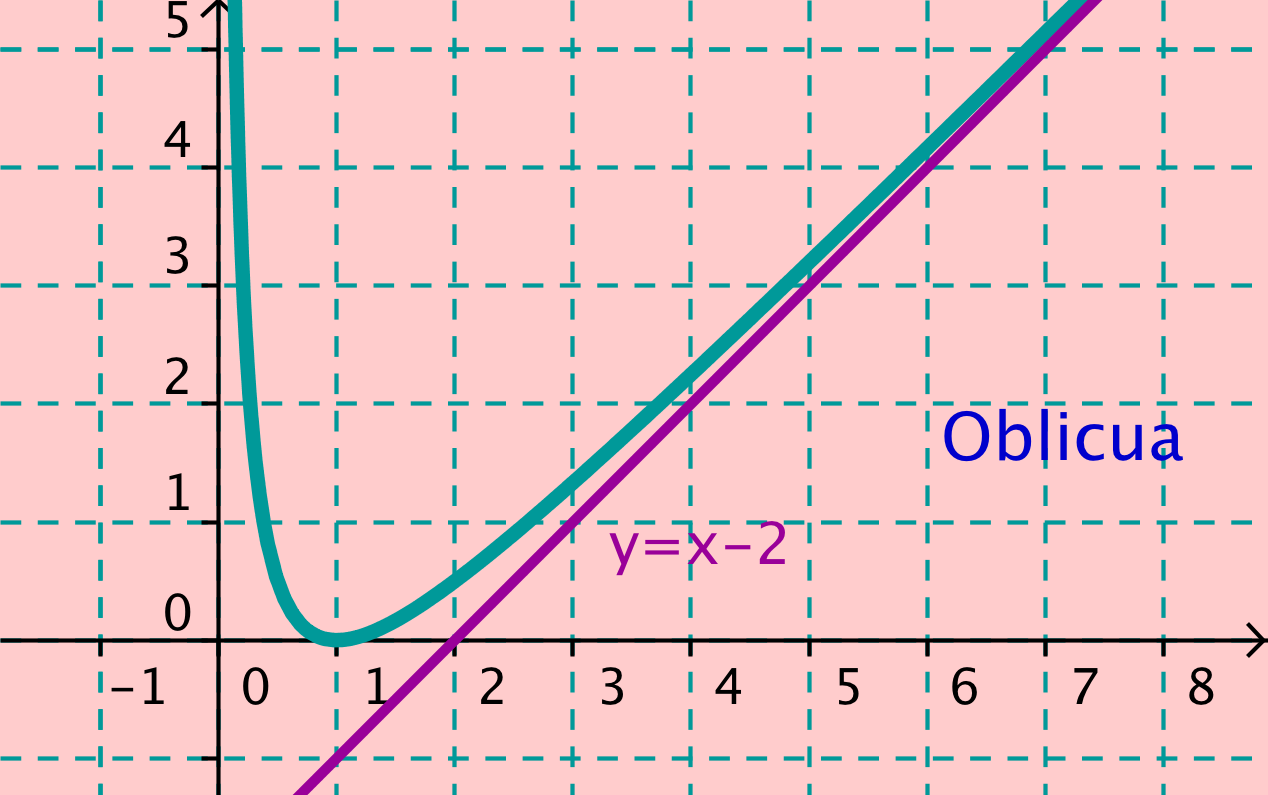
Como una asíntota es una recta, tenemos hasta tres posiciones distintas de una recta con relación a los ejes.
|
|
|
Por ello, para cada función pueden existir hasta tres tipos distintos de asíntota.
La vertical existirá si el límite de la función tiende a infinito cuando x tiende a un valor finito a, su valor será x=a.
La horizontal y la oblicua las encontraremos cuando estudiemos lo que ocurre cuando la variable independiente tienda a más o menos infinito.
En el caso de funciones racionales podemos hacer un estudio particular para saber que tipos de asíntotas tendrán según sean el numerador y el denominador. Veámoslo en la siguiente presentación. Pulsa sobre la imagen para ir pasando de página.
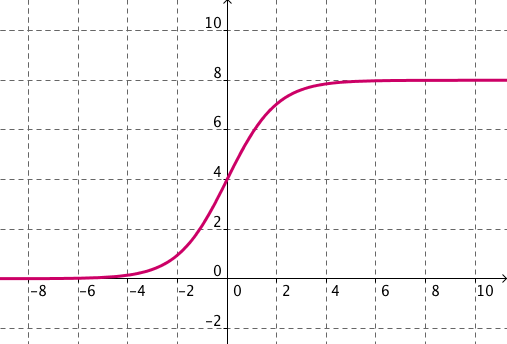
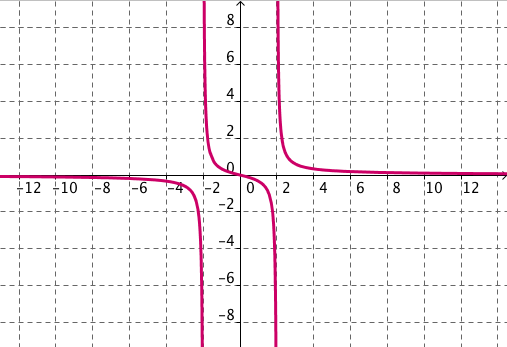
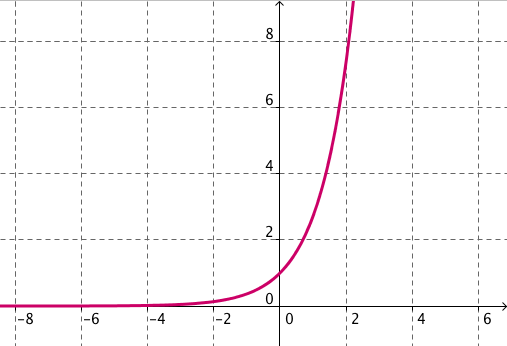
Señala las asíntotas de cada una de las siguientes funciones. Para ello rellena los espacios de la forma x=2 si es vertical, y=-3 si es horizontal e y=2x+1 si es oblicua. En caso de que no tenga alguna de ellas escribe no. Pondremos dos asíntotas verticales por si hay más de una.
| apartado (a) | apartado (b) |
apartado (c) | apartado (d) |
 |
 |
 |
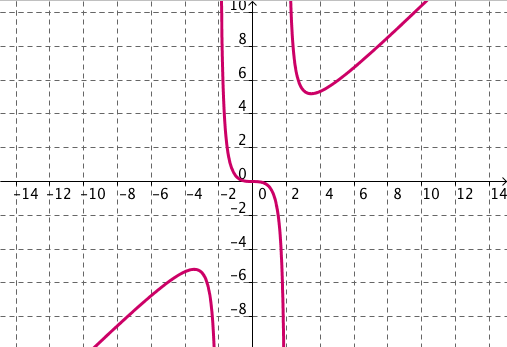 |
apartado (a)
vertical1 ; vertical2 ; horizontal en -∞ ; horizontal en +∞ ; oblicua en -∞ ; oblicua en +∞ ;
apartado (b)
vertical1 ; vertical2 ; horizontal en -∞ ; horizontal en +∞ ; oblicua en -∞ ; oblicua en +∞ ;
apartado (c)
vertical1 ; vertical2 ; horizontal en -∞ ; horizontal en +∞ ; oblicua en -∞ ; oblicua en +∞ ;
apartado (d)
vertical1 ; vertical2 ; horizontal en -∞ ; horizontal en +∞ ; oblicua en -∞ ; oblicua en +∞ ;