1.1. Se mira pero no se toca
En ocasiones, al acercarnos a un punto por la izquierda o por la derecha, la función crece indefinidamente.
Sea a un número real, la recta vertical x=a es una asíntota vertical de la función y=f(x) si se verifica alguna de las siguientes propiedades:
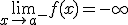 |
 |
 |
 |
 |
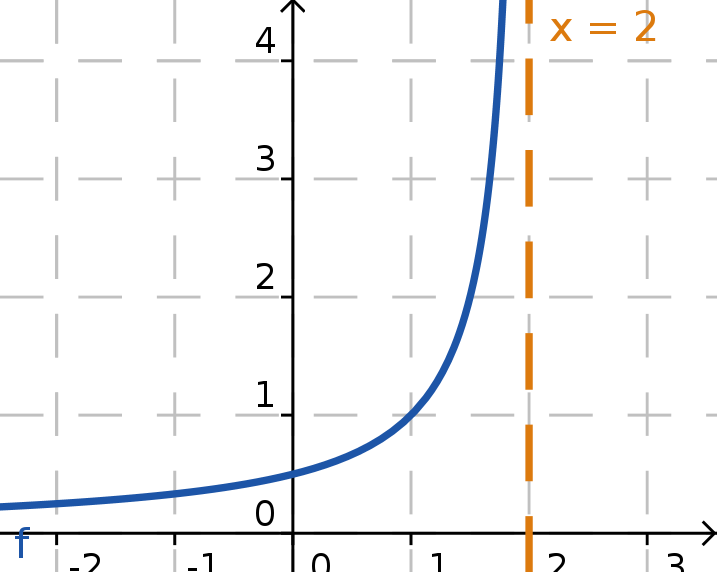 |

|
 |
¿Cómo saber donde buscar la asíntota vertical?
- Si es una función polinómica, no tiene asíntotas de ningún tipo.
- Si es una función racional, como vimos en el apartado anterior, tendremos que buscar en las raíces del denominador.
- Otra función que tiene asíntota vertical es la función logarítmica, más concretamente, en los puntos extremos de los intervalos donde empieza el dominio.
| y=ln(x) |
|
|
|
El logaritmo tiene una asíntota vertical x=0
|
Tenemos la función 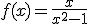 y queremos calcular sus asíntotas verticales,
y queremos calcular sus asíntotas verticales,
Calcula, si las tienen, las asíntotas verticales de las siguientes funciones:
 |
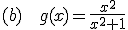 |
 |
Otra función que presenta asíntotas verticales es la función tangente. Esta función asocia a cada valor de x la tangente de dicho ángulo x.
La gráfica es la que sigue y como puedes ver, tiene infinitas asíntotas verticales, en todos los puntos de la forma:
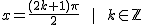

Si quieres saber más sobre la tangente de un ángulo y la función tangente sigue este enlace.


 ya que cuando tomamos valores muy próximos a 1 por la derecha, el
numerador tiende a 1 y el denominador a 0, pero por la derecha, es
decir, valores positivos. Por lo tanto, el límite es más infinito. La
asíntota vertical es como la última imagen de la definición.
Cuando nos acercamos a x=1 por la derecha la gráfica de f(x) tiende a
+∞.
ya que cuando tomamos valores muy próximos a 1 por la derecha, el
numerador tiende a 1 y el denominador a 0, pero por la derecha, es
decir, valores positivos. Por lo tanto, el límite es más infinito. La
asíntota vertical es como la última imagen de la definición.
Cuando nos acercamos a x=1 por la derecha la gráfica de f(x) tiende a
+∞.
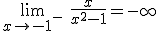 . Estamos en el caso 2 de la definición. Cuando nos acercamos a x=-1 por la izquierda la gráfica de f(x) tiende a -∞.
. Estamos en el caso 2 de la definición. Cuando nos acercamos a x=-1 por la izquierda la gráfica de f(x) tiende a -∞.
 ,
esto es, es similar a la tercera gráfica de la definición. Cuando nos
acercamos a x=-1 por la derecha, la gráfica de f(x) tiende a
+∞.
,
esto es, es similar a la tercera gráfica de la definición. Cuando nos
acercamos a x=-1 por la derecha, la gráfica de f(x) tiende a
+∞.
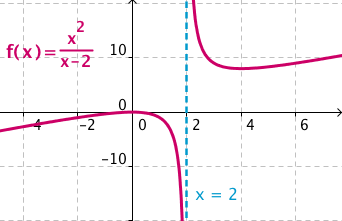
 . Por lo tanto, tiene una asíntota vertical en x=2.
. Por lo tanto, tiene una asíntota vertical en x=2.

 .
.