2. La solución es la S
|
| Imagen de Staphylococcus con licencia Creative Commons |
 |
| Imagen en Wikimedia Commons |
El economista británico Thomas Malthus propuso en 1798 que el crecimiento de una población se puede considerar como un proceso continuo, cuya velocidad de aumento es proporcional a la población ya existente.
Si C es la población inicial, existe una constante a en cada población, de manera que el número de individuos al cabo de un tiempo x, viene expresada por una ley del tipo: P(x)=C·ax
Si aplicamos esta fórmula al estudio de crecimiento de bacterias nos puede ocurrir algo como lo siguiente:
Supongamos que tenemos 500 bacterias en una placa de Petri. Una hora después comprobamos que su número ha aumentado hasta 800.
P(1)=800= 500 · a1 . Despejamos, a1=8/5. Por lo tanto, a=8/5=1,6
Luego la fórmula nos queda como P(x)=500·(1,6)x .
Si lo dejamos en el laboratorio y nos vamos una semana de vacaciones , a la vuelta tendríamos 9,8·1036 ejemplares, aproximadamente 1037 individuos. Si una bacteria ocupa 4 micras cúbicas, 4·10-18 m3 todas ocuparían un volumen de 4*1019 m3
Recuerda que el volumen de la luna es aproximadamente 2,1958*1019 m3. Es decir, tendríamos 1,78 veces el volumen de la luna.
En realidad lo que ocurre es que las poblaciones encuentran un nivel de saturación, que no pueden sobrepasar por dificultades de espacio, de alimento o de otros condicionantes.
Importante
La función que representa esta situación es:
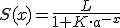
llamada función logística, o función sigmoide (la gráfica de la función tiene forma de S). L es la población límite y K=(L/C-1). Recuerda que a es un valor característico de cada población y C es la población inicial.
Esta función tiene una asíntota horizontal cuando x →+∞ en y=L, pues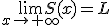
, es decir, al cabo de un tiempo la población se estabiliza cada vez más cerca del valor de L.
Volvamos con nuestro ejemplo. Si la población límite es L=107 bacterias. K=19999. Recordemos que a=1,6. Vamos a representar las dos funciones en una misma gráfica para ver la diferencia. Al principio son parecidas, pero a partir de las 10 horas, los cambios son muy significativos.
AV - Reflexión
 |
| Imagen de nblumhardt con licencia Creative Commons |
Se realiza un experimento para introducir conejos en un habitat donde no existen. Las condiciones de este habitat hacen que la capacidad de reproducción de la especie esté en el 20% mensual.
Para ello se llevan 200 individuos de esta especie. Por problemas de recursos alimenticios, no pueden vivir en este habitat más de 4000 individuos.
Haz un estudio de la evolución del número de conejos por trimestre durante los primeros 5 años según la función exponencial y según la función logística. Haz una tabla donde aparezcan los resultados y la diferencia entre ambos cálculos.
Escribe la ecuación de la asíntota en +∞ de la función logística y comprueba que coincide con el nivel de saturación.
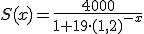
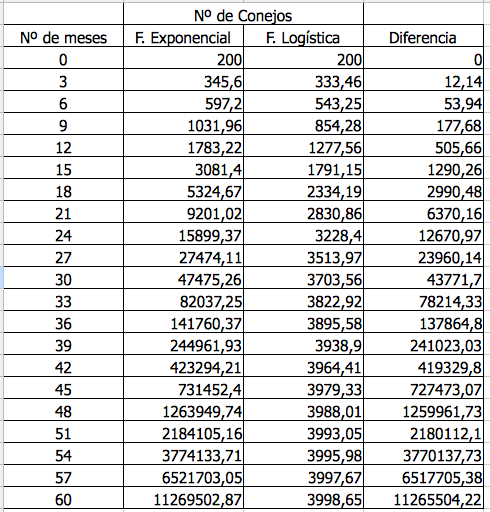
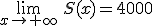, por lo tanto la ecuación de la asíntota es y=4000. En la tabla puedes observar que los valores de la función logística se estabilizan alrededor de este valor al aumentar el número de meses.