1.2. En infinito
 |
| Imagen de Goldmund100 bajo licencia Creative Commons |
Vamos a volver a viaje de Córdoba que le íbamos a regalar a Juan. Resulta evidente que mientras más personas entre en el regalo a menos cantidad caben. El viaje con todos los gastos incluidos sale por 400 €, así que si inicialmente el regalo se lo hacían las ocho personas que compartían departamento con él, cada una cabía a 50 €. Si lo hacemos extensivo a las 20 personas que trabajan en la delegación de Córdoba de TRANS VELOX, cada uno salimos a 20 € y si además entran los amigos del bar donde suele desayunar Juan, ya somos 30 personas y cabemos sólo a 13,33 €. Y si seguimos metiendo gente, cada vez cabremos a menos, si entran los 2000 vecinos del barrio, ya cabemos a 20 céntimos (0,20 €), y ya puestos a exagerar, si en el regalo entran los generosos 328.428 habitantes de Córdoba, cada uno pagará la impresionante cifra de 0,00122 €, es decir, 0,1 céntimos de euro aproximadamente.
Esta situación, se expresaría mediante la función 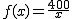 , donde x indicaría el número de personas y f(x) la cantidad a pagar cada una. Como hemos visto, mientras mayor sea el número de personas, menor es la cantidad a pagar, acercándose ésta cada vez más cero. Con límites, decimos que f(x) tiende a 0 si x tiende a infinito (a + infinito) y lo escribimos así:
, donde x indicaría el número de personas y f(x) la cantidad a pagar cada una. Como hemos visto, mientras mayor sea el número de personas, menor es la cantidad a pagar, acercándose ésta cada vez más cero. Con límites, decimos que f(x) tiende a 0 si x tiende a infinito (a + infinito) y lo escribimos así:
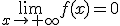
Por tanto, como ya habíamos avanzado en el punto anterior, los límites no sólo se ven en puntos concretos, sino que podemos observar la tendencia de la función si en el eje de abscisa nos alejamos mucho, tanto a valores positivos como negativos, y el resultado de estos límites serán números reales o también infinito.
En la siguiente escena te presentamos cinco funciones, pulsando sobre el control "función" va cambiando de una otra. Ve pasando por todas las funciones y averigua cuál es el límite cuando x tiende a -∞ y a +∞.
Applet Descartes de M.ª Jesús Pasarín Vázquez bajo licencia Creative Commons.
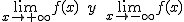 y para ello, debes observar la tendencia de la función cuando nos vamos alejando por el eje X. Si pulsas sobre el control x, un punto se va desplazando por la gráfica y puedes observar en la esquina izquierda el valor de las coordenadas. Además, si te hace falta puedes usar el zoom y los controles O.x y O.y para visualizar la función.
y para ello, debes observar la tendencia de la función cuando nos vamos alejando por el eje X. Si pulsas sobre el control x, un punto se va desplazando por la gráfica y puedes observar en la esquina izquierda el valor de las coordenadas. Además, si te hace falta puedes usar el zoom y los controles O.x y O.y para visualizar la función.
 |
| Imagen de art_es_anna bajo licencia Creative Commons |
Y ahora vamos a resolver el asunto de las florecillas. Si recuerdas, teníamos 30.000, cada una ocupaba 1 cm2 y por tanto nuestra alfombra ocuparía 30.000 cm2. Si le llamamos "y" a la largura de la alfombra y "x" a la anchura, tendríamos que la relación entre las dos variables es:
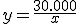 o bien
o bien 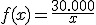
Fíjate que si le damos 100 cm de ancho, el largo sería 300 cm, si le damos 50 cm de ancho, el largo sería 600 cm, si le damos 1 cm de ancho el largo 30.000 y si seguimos acortando la anchura la largura sigue creciendo, por ejemplo, si le damos 0,5 cm de ancho, saldría una altura de 60.000 cm y si le damos 0,1 cm el largo sería de 300.000 cm. O sea, que cuanto más me acerco a cero en la anchura, mayor es el resultado de la largura. O sea, que ahora en lugar de acercarse la función a un valor se dispara hasta el infinito, luego con límites, lo escribiremos así:
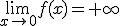
Aunque para ser más exactos, deberíamos escribir límite por la derecha, pues nos estamos acercando a cero por valores mayores que él.
Calcula los siguientes límites a partir de la gráfica que te proponemos:
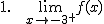 |
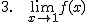 |
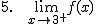 |
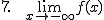 |
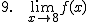 |
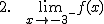 |
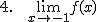 |
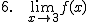 |
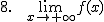 |
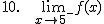 |
 |
| Imagen en Wikimedia Commons bajo licencia Creative Commons |
John Wallis, (1616 - 1703) matemático inglés, fue el que introdujo el símbolo ∞ para representar la noción de infinito en su obra "Arithmetica Infinitorum".
A Wallis se le atribuye en parte el desarrollo del cálculo moderno. Fue el precursor del cálculo infinitesimal que estamos empezando a ver con los límites.
Entre 1643 y 1689 fue criptógrafo del Parlamento y posteriormente de la Corte real. Fue también uno de los fundadores de la Royal Society y profesor en la Universidad de Oxford.
Al margen de sus trabajos en matemáticas, también escribió sobre teología, lógica, gramática inglesa y filosofía; asimismo, fue uno de los pioneros en la introducción en Inglaterra de un sistema de enseñanza para sordomudos, inspirado en el método del español Juan de Pablo Bonet.
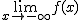 = -∞
= -∞ 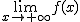 = - ∞
= - ∞