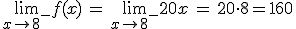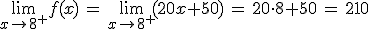3. Nunca nos separaremos
 |
| Imagen de Daquellamanera bajo licencia Creative Commons |
Si recuerdas del primer tema de la unidad, dijimos que una función era continua si no tenía ninguna interrupción; si se podía dibujar de un trazo sin levantar el lápiz del papel. Esto es una visión global de la continuidad, pero cuando no hay continuidad es porque esta propiedad falla en un determinado lugar. ¿Y qué será lo que falla?
Ha llegado el momento de juntar límite y continuidad y de ver la continuidad de una función pero sin necesidad ya de tener que ver la gráfica por delante. De momento, vamos a comenzar recordando las tres posibilidades de discontinuidad que vimos en el tema 1 de la unidad.
 |
 |
|
| Discontinuidad evitable |
Discontinuidad de salto infinito |
Discontinuidad de salto finito |
Vamos a comenzar con la primera. ¿Por qué se produce una discontinuidad evitable?
Si te fijas en la primera gráfica, si nos acercamos en el eje X a 1, la función, tanto por la izquierda como por la derecha de 1, se acerca a -7. El problema está en que justo cuando llegamos al valor x=1, la función se va al 2 en lugar de -7. Por tanto, lo que ocurre aquí es que límite e imagen de la función no coinciden:
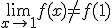
Si te fijas, en todos los otros puntos esto sí se cumple, el límite de la función coincide con el valor de la imagen.
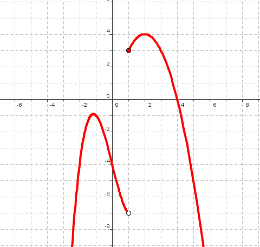
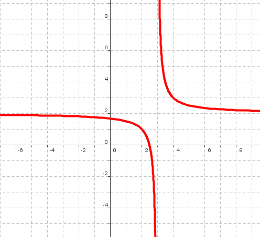
La segunda discontinuidad que aparece es la de salto infinito. ¿Por qué en x=3 hay una discontinuidad de salto infinito? La respuesta es clara, porque cuando nos acercamos a x=3, la función se va hacia infinito; a -∞ por la izquierda y a +∞ por la derecha, o sea, cuando al hacer el límite en el punto el resultado es infinito:
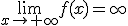
Si recuerdas, esto ocurría en las indeterminaciones k/0.
Por último, la tercera gráfica no es continua porque en x=1 hay un salto. ¿Qué es lo que ocurre para que haya esa discontinuidad de salto finito? Pues que cuando nos acercamos a 1, la función se acerca a distintas cosas según por el lado que lo hagamos, por la izquierda se acerca a -7 y por la derecha a 3. Luego, lo que ocurre, es que los dos límites laterales existen, son números reales, pero no coinciden.
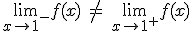
Si te fijas en todos los otros puntos esto sí se cumple, los límites laterales coinciden.
Teniendo en cuenta lo que acabamos de ver, una función es continua en x = a si:
- Existe f(a).
- Los dos límites laterales existen, son números reales y coinciden.
- El valor del límite coincide con el de la imagen.
Esas tres propiedades se resumen en: 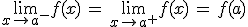
En general, todas las funciones elementales, las que has visto en el tema anterior, son continuas en sus respectivos dominios de definición.
 |
| Imagen en blogdenoelia bajo licencia Creative Commons |
En este ejercicio, vamos a ver cómo estudiar la continuidad de una función a trozos sin necesidad de ver su representación gráfica. ¿Recuerdas el ejemplo de los sueldos de los camareros de la caseta que vimos en el apartado 2?
Teníamos que la función que le daba a Nacho el dinero a pagar a cada camarero de la caseta según las horas que trabajaba era:
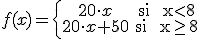
¿Será esa una función continua?
La función f(t) que mostramos a continuación muestra el beneficio de la empresa EXRED (en cientos de miles de euros) a lo largo de los diez primeros años tras su fundación. La función donde t expresa el tiempo en años es:
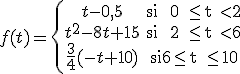
¿Es continuo el crecimiento de los beneficios de la empresa?
En este vídeo te mostramos cómo calcular una incógnita o dos dentro de una función a partir de la idea de que la función tiene que ser continua. Este ejercicio es de los clásicos de selectividad, así que si estás pensando en ello, debes verlo y entenderlo:
Si quieres hacer algunos ejercicios de este estilo, en este enlace encontrarás varios.