2. Algo más rápido, please!
 |
| Imagen en blogdenoelia bajo licencia Creative Commons |
Nacho el chico, que lleva la gestión económica de la caseta TRANS VELOX en la feria de Córdoba, tiene controlado el gasto que ha de hacer la caseta en pagar a los camareros. Cada camarero o camarera gana 20 euros por cada hora de trabajo más un fijo de 50 euros si trabaja al menos 8 horas.
Si llamamos x al tiempo trabajado (en horas), la función que nos da el dinero a pagar a cada camarero dependiendo del tiempo trabajado es:
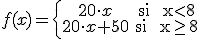
¿Cuánto gana si trabaja 4 horas?¿Y si trabaja 10? ¿Y con 8 horas?
Estudia también los límites para x=4, x=10 y x=8.
Regla I
Para calcular el límite de una función, cuando x tiende a x0, basta con sustituir x0 en la función y si nos da un número, es decir, se pueden hacer todas las operaciones, ese es el resultado del límite.
Regla II
En una función a trozos, para calcular el límite en el punto donde se corta la función, hay que hacer los límites laterales y para ello sustituir en los trozos adecuados.
 |
| Imagen de Torley bajo licencia Creative Commons |
¿Te imaginas un supercamarero que trabaje horas y horas sin parar? ¿Cuánto ganaría?
La respuesta creo que es evidente, ¿no? Un pastón. Claro, a más trabajo más gana. Pero vamos a ver que efectivamente es así. Esta situación tan irónica respondería a calcular el límite cuando x tiende a +∞, pues estamos dándole valores grandes a x, al tiempo trabajado.
Si hacemos lo mismo que en el ejercicio anterior, habría que coger una secuencia de números cada vez mayores, por ejemplo 100, 1.000 y 10.000. Vamos a ver lo que ocurre.
Regla III
Las funciones polinómicas, cuando x tiende a +∞ o -∞, se comportan del mismo modo que su término de mayor grado:
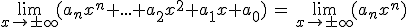
Elige la opción correcta en los límites que aparecen a continuación.
1) 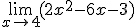
|
-11
| |
|
-7
| |
|
5
|
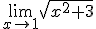
|
2
| |
|
4
| |
|
0
|
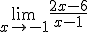
|
0
| |
|
-8
| |
|
4
|
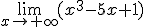
|
+∞
| |
|
-∞
| |
|
No existe
|
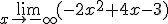
|
+∞
| |
|
-∞
| |
|
0
|
Aparte de las polinómicas, en la Ciencias Sociales, muchas cuestiones responden a funciones exponenciales y logarítmicas, así que no está de más que conozcas el comportamiento de estas funciones.
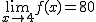
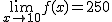 .
.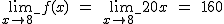
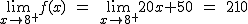
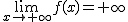 , pero vamos a sacar el porqué.
, pero vamos a sacar el porqué.
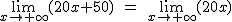 Y ahora procedemos así: Si sustituimos x por un número grande positivo, obtenemos un número grande positivo, y multiplicado por 20, un número más grande y positivo, luego,
Y ahora procedemos así: Si sustituimos x por un número grande positivo, obtenemos un número grande positivo, y multiplicado por 20, un número más grande y positivo, luego,