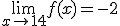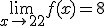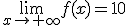1.1. Con gráficas
Ejemplo o ejercicio resuelto
 |
| Imagen de tonnoro bajo licencia Creative Commons |
En las cocinas de las casetas de feria, es importantísimo cuidar la seguridad en la manipulación de los alimentos. A la caseta de TRANS VELOX ha llegado una partida de carne, y previendo que no se va a gastar en ese día, se meten en el congelador que tienen allí. Se congelan a dos grados bajo cero y al cabo de las 14 horas se saca y se guardan en una nevera que mantiene algo el frío para que al cabo de unas ocho horas está en condiciones de poderse usar.
La siguiente gráfica muestra la evolución de la temperatura a la que se encuentran las cajas según va pasando el tiempo:
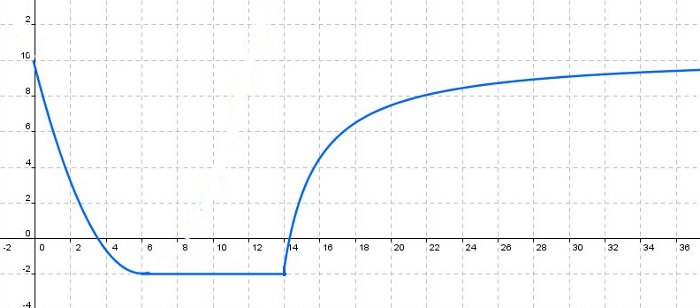
¿Qué ocurre si miramos alrededor de las 14 horas? ¿Y de las 22 horas? ¿Y si dejamos la caja en esa segunda nevera indefinidamente?
Fíjate en la siguiente escena. Pulsa sobre el botón "play" y observa la secuencia que hace la gráfica para calcular el límite cuando x tiende a 0. Esa secuencia es la que debes recorrer tú cuando quieras calcular un límite.
Applet Descartes de José Manuel Gallardo Morilla bajo licencia Creative Commons.
Actividad
Observa ahora esta escena. Haz lo mismo, pulsa sobre el botón "play" y observa lo que ocurre en la gráfica cuando nos acercamos a 0 en el eje X.
Applet Descartes de José Manuel Gallardo Morilla bajo licencia Creative Commons.
Esta función es una de las que has visto en el tema anterior y en el curso pasado, una función a trozos que se está cortando en 0, y fíjate que según por el lado que nos acerquemos a cero, la función se acerca a un valor u otro. Si lo hacemos por la izquierda, la función se acerca a -1, mientras que si lo hacemos por la derecha, los valores de la función se aproximan a 1.
Por tanto, es necesario indicar por qué lado nos estamos acercando al punto, y surge así el concepto de límite lateral.
Actividad
- Se llama límite lateral por la izquierda de la función f en el punto x0,al valor al que tiende la función cuando los valores de x que se aproximan a x0 son menores que x0. Lo expresamos con un signo - sobre el punto así:
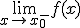
En el ejemplo,
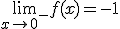
- Se llama límite lateral por la derecha de la función f en el punto x0,al valor al que tiende la función cuando los valores de x que se aproximan a x0 son mayores que x0. Lo expresamos con un signo + sobre el punto así:
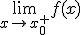
En el
ejemplo,
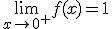
- El límite de una función en un punto existe si los dos límites laterales existen y coinciden. Así, en el ejemplo, el límite en 0 no existiría al no coincidir los límites laterales.
AV - Actividad de Espacios en Blanco
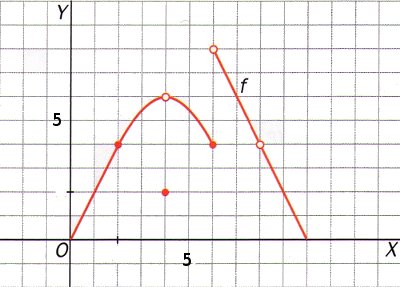
Calcula los siguientes límites a partir de esta gráfica. En caso de no existir escribe no
|
|
|
|
|
|
|
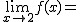
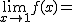
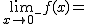
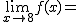
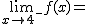
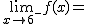
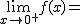
f(8)= |
|
|
|
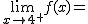
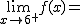
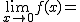
f(4)= |
|
|
|
|
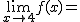
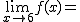
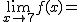
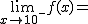