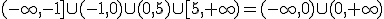4.4. La chaquetera
Una función 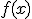 es una función definida a trozos cuando a lo largo de todos los números reales no queda definida mediante una única expresión, sino que dependiendo del tramo en el que nos encontremos adquiere una forma distinta. Un ejemplo de este tipo de funciones sería:
es una función definida a trozos cuando a lo largo de todos los números reales no queda definida mediante una única expresión, sino que dependiendo del tramo en el que nos encontremos adquiere una forma distinta. Un ejemplo de este tipo de funciones sería:
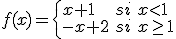
En este caso, para valores menores que 1 la función toma la expresión 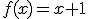 y para valores mayores o iguales que 1 la función toma la expresión
y para valores mayores o iguales que 1 la función toma la expresión 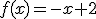 .
.
¿Cómo se representa este tipo de funciones?, pues tomando el trozo de representación gráfica de cada una de las expresiones que toma en el intervalo correspondiente. Así, para la función anterior, su representación gráfica sería:
|
|
| Función definida a trozos. Animación obtenida del banco de imágenes del ITE. |
En el caso de la función anterior tenemos que 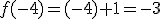 ya que -4 es menor que 1 y que
ya que -4 es menor que 1 y que 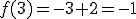 ya que 3 es mayor que 1 y por tanto se utiliza la segunda definición.
ya que 3 es mayor que 1 y por tanto se utiliza la segunda definición.
La anterior función está definida en dos trozos, pero una función definida a trozos puede tener tantos como se necesite. De este tipo de funciones podemos decir que:
1.- El dominio de la función es la unión de cada uno de los intervalos en los que está dividida, quitando de cada uno de ellos los valores en los que no esté definida la expresión correspondiente. Para ello te invitamos a que observes el ejercicio resuelto que aparece seguidamente.
2.- Los intervalos de crecimiento y decrecimiento, así como los máximos y mínimos dependen de cada una de las expresiones que toma.
Observa en el siguiente vídeo cómo se realizaría la representación gráfica de la función definida a trozos:
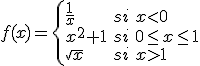
|
|
|
|
El Teatro romano de Mérida es una construcción promovida por el cónsul Marco Vipsanio Agripa, en la ciudad romana de Emerita Augusta, actual Mérida, España. Según fecha inscrita en el propio teatro su construcción se produjo en los años 16 a 15 a. C. Si quieres ver una imágen panorámica del teatro pulsa aquí y muévete por la ventana que aparece.
El teatro ha sufrido varias remodelaciones, la más importante, a finales del siglo I o principios del siglo II, posiblemente en época del emperador Trajano, cuando se levantó la actual fachada o frente de escena, y otra en época de Constantino entre los años 330 y 340, introduciéndose nuevos elementos arquitectónicos-decorativos y construyéndose una calzada que rodea el monumento.
Actualmente el Teatro de utiliza para representaciones teatrales en el festival de teatro de Mérida y para la celebración de conciertos culturales. En uno de esos conciertos a cargo del grupo Acetre y cuyas imágenes puedes contemplar en el vídeo, uno de los técnicos de sonido está tomando medida de los decibelios de sonido que se producen en el concierto en función del nivel de los graves que haya sintonizado. Según sus cálculos, la función que le resulta es la siguiente:
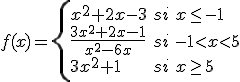
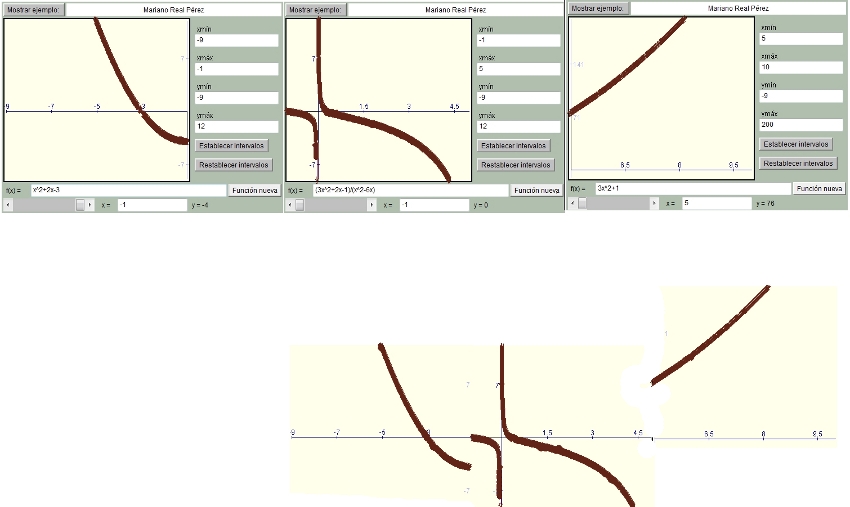
donde 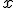 es el nivel de los graves. Pero está teniendo algunos problemas con alguna medida. Ayúdale a determinar el dominio de la función para saber con qué valores puede utilizarla. Utiliza la pantalla interactiva que aparece más abajo para hacer una representación en papel de la gráfica de la función.
es el nivel de los graves. Pero está teniendo algunos problemas con alguna medida. Ayúdale a determinar el dominio de la función para saber con qué valores puede utilizarla. Utiliza la pantalla interactiva que aparece más abajo para hacer una representación en papel de la gráfica de la función.
|
Applet interactiva obtenida de la aplicación "Patrimonio Matemático de los Pueblos" de Mariano Real Pérez. Contenido interactivo del ITE. Para obtener un manual detallado pulsa aquí |
Si tenemos la función
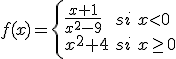
Calcula el dominio y realiza su representación gráfica utilizando la ventana interactiva que se encuentra encima de este enunciado
Un caso particular de función definida a trozos lo tenemos en la función valor absoluto. Sabemos que si 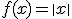 entonces:
entonces: 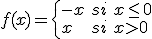 .
.
de igual manera tenemos que si 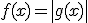 entonces:
entonces: 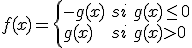
En la siguiente animación podemos ver cómo obtener la gráfica de 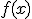 conociendo la de
conociendo la de 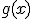 :
:
|
|
| Función valor absoluto. Animación obtenida del Banco de Imágenes del ITE. |
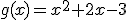 son todos los números reales según hemos visto en las funciones polinómicas, y como
son todos los números reales según hemos visto en las funciones polinómicas, y como 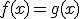 para los valores menores o iguales que -1, entonces el intervalo
para los valores menores o iguales que -1, entonces el intervalo 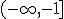 es parte del dominio de
es parte del dominio de 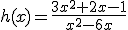 son todos los números reales excepto aquellos que anulan el denominador. calculamos los que anulan el denominador:
son todos los números reales excepto aquellos que anulan el denominador. calculamos los que anulan el denominador:
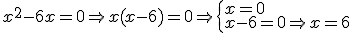
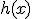 son todos los números menos el cero y el seis. Como
son todos los números menos el cero y el seis. Como 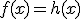 en
en 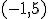 , los intervalos
, los intervalos 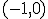 y
y 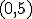 son parte del dominio de
son parte del dominio de 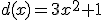 son todos los números reales según hemos visto en las funciones polinómicas, y como
son todos los números reales según hemos visto en las funciones polinómicas, y como 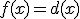 para los valores mayores o iguales que 5, entonces el intervalo
para los valores mayores o iguales que 5, entonces el intervalo 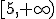 es parte del dominio de
es parte del dominio de