2. ¡Qué corte!
 |
Para representar gráficamente una función es fundamental conocer algunas de sus propiedades. A partir de ahora nos vamos a centrar en localizar distintos puntos característicos de las funciones que nos van a permitir conocerlas más de cerca y nos va a permitir discernir sobre su posible gráfica. Los puntos que localicemos de cada función son puntos por los que va a pasar su gráfica, pero además, son puntos que nos van a proporcionar información sobre algún caso concreto de la situación real de la que fue extraída esa función. Ahora debes estar atento. Ya verás como no es nada complicado.
Entre los puntos que podemos considerar como característicos de una función se encuentran los puntos de corte con los ejes. Estos puntos nos proporcionan información sobre la función. Puede parecer que esta información sólo se refiere a estos puntos de corte, pero en ocasiones nos pueden ayudar a determinar otros puntos importantes de la misma.
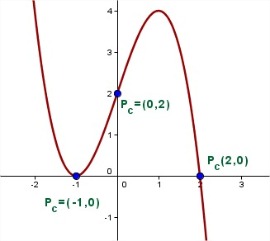
Si tenemos una función 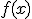 se llama punto o puntos de corte con el eje de abcisas a la/s soluciones del sistema de ecuaciones
se llama punto o puntos de corte con el eje de abcisas a la/s soluciones del sistema de ecuaciones 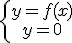 si el punto
si el punto 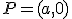 es una de las soluciones, por analogía con los polinomios, se dice que
es una de las soluciones, por analogía con los polinomios, se dice que 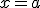 es una de la raíces de la función.
es una de la raíces de la función.
 |
Por otra parte, se llama punto de corte con el eje de ordenadas a la solución del sistema de ecuaciones 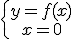 . Si este sistema tiene solución, la misma será un punto
. Si este sistema tiene solución, la misma será un punto 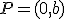 por el que pasa la gráfica de la función.
por el que pasa la gráfica de la función.
A diferencia de la anterior definición, aquí el sistema de ecuaciones a
lo sumo tiene una solución ya que, según hemos indicado en la
definición de función, al valor 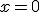 solamente le puede corresponder un único valor.
solamente le puede corresponder un único valor.
 |
| Montadora de neumáticos. Imagen obtenida del banco de imágenes del ITE. |
La empresa de Amelia ha comprado una montadora de neumáticos mecánica y desea automatizarla. Han lijado la máquina, la han pintado de rojo y el ingeniero industrial ha diseñado un mecanismo para automatizarla. Este mecanismo lleva incorporado un pequeño ordenador que controlará todo el proceso. el programador informático ha creado un programa que automatiza todo lo que se puede hacer con la rueda, pero ha detectado que la máquina va cometiendo un error que va en función del tiempo que se utiliza la máquina. Este error en función del tiempo viene expresado por la siguiente función:
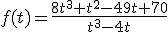
Este error no debe nunca ser 8 ¿Para qué valores del tiempo el error es 8?
Utiliza la pantalla interactiva que aparece más abajo para representar la función que hayas utilizado. Ahora la que aparece es 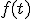 (ten cuidado al escribir la función que debe aparecer como variable x).
(ten cuidado al escribir la función que debe aparecer como variable x).
|
Applet interactiva obtenida de la aplicación "Patrimonio Matemático de los Pueblos" de Mariano Real Pérez. Contenido interactivo del ITE. Para obtener un manual detallado pulsa aquí |
|
|
| Gráfica de parábola. Animación obtenida del banco de imágenes del ITE |
Como hemos indicado anteriormente, en algunas ocasiones los puntos de corte nos proporcionan más información que meros puntos por los que pasa la gráfica de la función.
Este es el caso de la función parabólica
que podemos representar 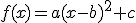 .
.
Comprueba en la ventana interactiva que aparece más abajo que si a=3, b=4 y c=-5, el punto medio de los dos puntos de corte de la función con el eje de abcisas es el valor en el que la función se hace más pequeña.
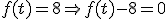 , es decir, debemos calcular los puntos de corte con el eje de abcisas de la función
, es decir, debemos calcular los puntos de corte con el eje de abcisas de la función 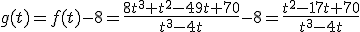
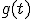 ya que no puede tomar valores que no estén en su dominio. En este caso, dado que la función es una fracción, podremos hacer la operación siempre que el denominador sea distinto de cero, es decir:
ya que no puede tomar valores que no estén en su dominio. En este caso, dado que la función es una fracción, podremos hacer la operación siempre que el denominador sea distinto de cero, es decir: 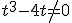 calculemos los valores que hacen cero el denominador:
calculemos los valores que hacen cero el denominador:
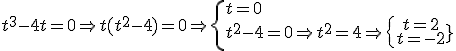
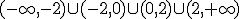
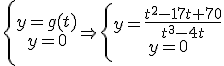
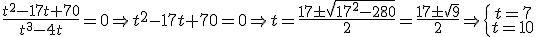
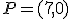 y
y 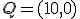
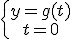
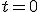 no está en el dominio de la función, luego este sistema no tiene solución, la función g(t) no corta al eje de las ordenadas. Esto equivale a decir que en ningún momento el error llega a ser 8.
no está en el dominio de la función, luego este sistema no tiene solución, la función g(t) no corta al eje de las ordenadas. Esto equivale a decir que en ningún momento el error llega a ser 8.