3. No seas monótono
Vamos a repasar ahora algunos conceptos sobre las funciones. Como todos ellos están relacionados de alguna manera, vamos a verlos todos a la misma vez, aunque cada uno lo recojamos en un apartado diferente.
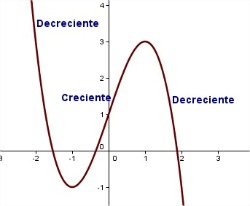
Todos ellos están relacionados con el comportamiento de la gráfica de la función, si es creciente, si es decreciente, cuándo se observa un extremo, es decir, un máximo o un mínimo...
Importante
 |
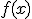decimos que es creciente si al dibujar su gráfica de izquierda a derecha el trazo cada vez es más alto. Por tanto, es creciente si al tomar dos valores 
y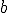 
cualesquiera, si 
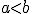entonces 
.
Si tenemos una función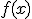
decimos que es decreciente si al dibujar su gráfica de izquierda a
derecha el trazo cada vez es más bajo. Por tanto, es creciente si al
tomar dos valores 
y 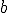cualesquiera, si 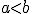entonces 
.
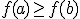Lo más normal es que la función no sea siempre creciente o decreciente, sino que se alternen los intervalos de crecimiento y de decrecimiento.
Importante
 |
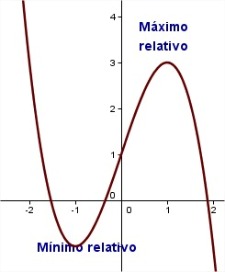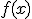tiene un máximo relativo en el punto 
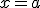si en todos los valores próximos a este punto, el valor de la función es más pequeño que 
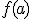o lo que es lo mismo, hasta el valor la función es creciente y después de este valor la función es decreciente.
Si para todos los valores 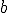se cumple que 
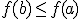, entonces se dice que tiene un máximo absoluto en .
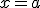Si tenemos una función 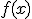tiene un mínimo relativo en el punto 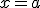si en todos los valores próximos a este punto, el valor de la función es más grande que 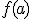o lo que es lo mismo, hasta el valor la función es decreciente y después de este valor la función es creciente.
Si para todos los valores 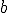se cumple que 
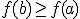, entonces se dice que tiene un mínimo absoluto en .
|
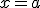Applet interactiva obtenida de la aplicación "Patrimonio Matemático de los Pueblos" de Mariano Real Pérez. Contenido interactivo del ITE. Para obtener un manual detallado pulsa aquí |
|
|
El siguiente vídeo te puede ayudar a comprender todos los conceptos anteriores y cómo se traducen éstos en la gráfica de la función. Observa que en cada uno de los tramos que recorre el ciclista, en la parte inferior de la pantalla aparece información sobre la propiedad de la gráfica en ese tramo o en ese punto en el que se encuentra el ciclista.
Las asíntotas de las que te habla las estudiaremos en el próximo tema.
Ejemplo o ejercicio resuelto
 |
| Imagen de Alessandro Quisi tomada del Banco de Imágenes del ITE. |
En una de las lijadoras que están automatizando en la empresa de Amalia han comprobado que la cantidad de líquido que debe circular por el inyector debe ser 12 unidades mas el triple de uno de los valores que resulta de un cálculo que proporcionan ciertas medidas del objeto que se quiere lijar.
Calcula la función que proporciona la cantidad de líquido en función del valor proporcionado por el cálculo y comprueba si es creciente o decreciente. Represéntala gráficamente en la ventana interactiva que se encuentra más arriba.
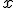es el valor proporcionado por el cálculo, la función que indica la cantidad de líquido en fución de ese valor es:
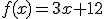
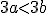y por tanto 
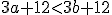luego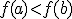 
, es decir, la función es creciente.