4.1. Todo seguido
Importante
Si tenemos una función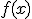 
decimos que es una función polinómica si tiene la forma
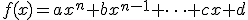
Estas funciones son las más sencillas que existen y de ellas podemos destacar que:
1.- Su dominio son todos los números reales ya que las operaciones que aparece en la función son sumas y productos y estas operaciones siempre se pueden hacer se trate del número que se trate.
2.- Siempre cortan al eje de las ordenadas.
3.- Si cortan al eje de abcisas en varios puntos, entre dos de esos puntos consecutivos existe un máximo o un mínimo.
4.- Sabemos que un polinomio de grado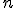 
tiene a lo sumo 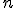raíces, por tanto, una función polinómica de grado 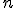corta al eje de abcisas a lo sumo en 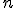puntos.
Pero para observar todas estas propiedades vamos a utilizar varios ejemplos.
Galería de funciones polinómicas
f(x)=2x+2
|
f(x)=-x²+2x+3
|
f(x)=x3+x²-4x-4
|
f(x)=x4-2x3-4x²+5x+2
|
AV - Actividad de Espacios en Blanco
Representa las siguientes funciones polinómicas en el recuadro interactivo que aparece más abajo e indica el punto de corte con el eje de las ordenadas, el número de máximos relativos que tiene, el número de mínimos relativos, si tiene máximo absoluto o si tiene mínimo absoluto y si es una función par o una función impar y el número de puntos en los que corta al eje de abcisas.
No solamente deberás escribir la función, sino que deberás ajustar los valores xmás, ymás, xmín e ymín para poder ver la función completamente.
En los huecos correspondientes a máximo u mínimo absoluto, función par o impar escribe sí o no según corresponda.
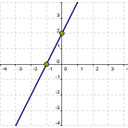
1.-
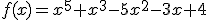
El punto de corte con el eje de las ordenadas es P=( , ), tiene máximos relativo, tiene mínimos relativo, tiene máximo absoluto, tiene mínimo absoluto, es una función par y es una función impar. Además corta al eje de abcisas en puntos.
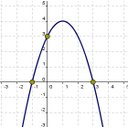
2.-
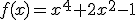
El punto de corte con el eje de las ordenadas es P=( , ), tiene máximos relativo, tiene mínimos relativo, tiene máximo absoluto, tiene mínimo absoluto, es una función par y es una función impar. Además corta al eje de abcisas en puntos.
|
Applet interactiva obtenida de la aplicación "Patrimonio Matemático de los Pueblos" de Mariano Real Pérez. Contenido interactivo del ITE. Para obtener un manual detallado pulsa aquí |
Curiosidad
Observa ahora lo que le ocurre a la gráfica de una función polinómica de grado 1 si introducimos la raiz cuadrada. Representa varias funciones de la forma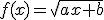 
en la siguiente ventana interactiva:
|
|
| Representación gráfica. Animación obtenida del banco de imágenes del ITE. |