2.2. ¿Cómo le damos la vuelta a una matriz?
|
|
Observa los precios de tres prendas de vestir que hemos seleccionado en unos almacenes:
El precio de cada prenda varía si es el precio normal, el precio en rebajas o el precio super-rebajado. Así observamos un cuadro de precios como el que sigue:
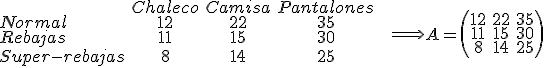
Si en el centro comercial las ventas de cada una de las prendas en cada uno de los trimestres fueron las que se recogen en el siguiente cuadro:
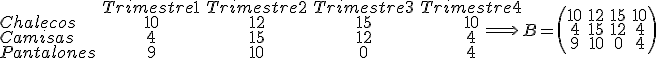
Para conocer la cantidad de dinero que ganaríamos en cada trimestre dependiendo de si ese trimestre los precios son los normales, es un trimestre de rebajas o es un trimestre de super-rebajas, solamente necesitaríamos multiplicar la primera matriz por la segunda:
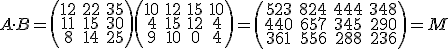
Según lo anterior, tendríamos que la cantidad de dinero ganada por trimestre dependiendo de si ese trimestre era normal, de rebajas o de super-rebajas es:
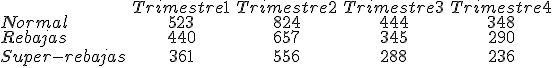
 |
| Centro comercial. Imagen obtenida del banco de imágenes del ITE. |
De esta forma, si el centro comercial hubiera estado de rebajas el segundo trimestre habría ganado 657€ con la venta de chalecos, camisas y pantalones.
En este caso conocíamos la matriz de precios A y la matriz de ventas por trimestre B y hemos podido calcular con una simple operación la matriz de ganacias M. Pero, ¿cómo podríamos calcular la matriz B si conociéramos la matriz A y la matriz M? Para responder a esta pregunta, imagina que tuviéramos una matriz F de forma que al multiplicar F por A resultara la matriz identidad. En ese caso tendríamos:
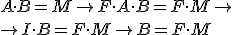
Si tuviésemos la matriz F ya lo tendríamos solucionado.
Dada una matriz cualquiera 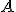 llamamos inversa de
llamamos inversa de 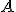 a otra matriz que denotaremos
a otra matriz que denotaremos 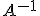 que cumpla que:
que cumpla que:
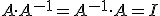
donde  es la matriz identidad.
es la matriz identidad.
 |
| Ojo. Imagen tomada del banco de imágenes del ITE. |
De la igualdad anterior podemos deducir que si la matriz  tiene orden
tiene orden 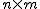 y la matriz
y la matriz 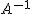 tiene de orden
tiene de orden 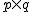 :
:
1.- Como debemos multiplicar 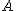 por
por 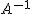 entonces
entonces 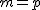 .
.
2.- Como debemos multiplicar 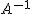 por
por  entonces
entonces 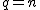 .
.
3.- Como el resultado de ambos productos debe ser la matriz identidad que es una matriz cuadrada entonces 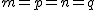 , por tanto , para que una matriz tenga matriz inversa, debe ser una matriz cuadrada
, por tanto , para que una matriz tenga matriz inversa, debe ser una matriz cuadrada
 no puedes ser cero ya que el determinante de la matriz identidad es 1.
no puedes ser cero ya que el determinante de la matriz identidad es 1.
Comprueba ahora lo que has aprendido marcando las opciones que sean correctas.
Dada una matriz 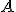 sabemos que:
sabemos que:
1.- Para que tenga inversa debe ser cuadrada.
| |
2.- Si tiene orden 3x2, la matriz inversa tiene orden 2x3
| |
3.- El determinante de la matriz debe ser distinto de cero.
| |
4.- 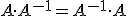
| |