2.1. ¿Cómo le damos la vuelta a un número?

|
| Número. Imagen obtenida del banco de imágenes del ITE. |
Vamos a comenzar por un caso simple del que ya conocemos como funciona.
Si elegimos un número cualquiera, nos encontramos con una caso especial de una matriz cuadrada de orden 1. En este caso vamos a practicar con la matriz
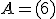
Buscamos una matriz B, de forma que al multiplicarla por la matriz A, nos resulte la matriz identidad, en este caso de orden 1, es decir:
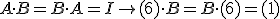
 |
| Número. Imagen obtenida del banco de imágenes del ITE |
En este caso sabemos que 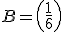
Según lo que conoces de la parte de números, sabes que a B se le denomina el inverso de A y que se representa como
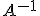 es decir
es decir 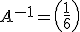
Por tanto, para el caso de los números y el producto de números es fácil encontrar el inverso ya que el inverso de un número 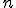 es
es 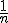 . Pero esto es así siempre que el número
. Pero esto es así siempre que el número 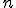 sea distinto de cero. El cero es el único número que no tiene inverso.
sea distinto de cero. El cero es el único número que no tiene inverso.
Marca las respuestas correctas.
Dado un número cualquiera 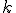
El inverso es 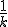 siempre siempre
| |
Al multiplicar 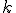 por su inverso el resultado siempre es 1. por su inverso el resultado siempre es 1.
| |
Al multiplicar el inverso de 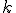 por el número por el número 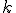 el resultado siempre es 1 el resultado siempre es 1
| |
El número 0 no tiene inverso.
| |
El inverso de cero es cero
| |
El inverso del inverso de 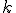 es el mismo número es el mismo número 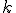 . .
| |