3. Especial selectividad
|
|
|
|
Ahora te proponemos unas serie de ejercicios aparecidos en selectividad relacionados con la matriz inversa o el rango de matrices de cara a que te sirvan de preparación de esta prueba. Recuerda que, como te hemos indicado en los temas anteriores, estos ejercicios no forman parte de tu formación a distancia sobre este tema, sino para profundizar por si fuera de tu interés preparar la selectividad. Aunque recuerda que los procesos de resolución son los mismos que utilizas en los ejercicios que debes hacer, por lo que quizás te sirvan de práctica.
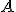 una matriz cuadrada que cumple que
una matriz cuadrada que cumple que 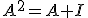 donde
donde 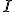 es la matriz identidad. Demuestra que la matriz
es la matriz identidad. Demuestra que la matriz 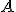 tiene inversa
tiene inversa
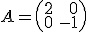 y
y 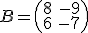 .
.
Calcula una matriz 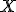 de forma que
de forma que 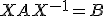 .
.
Dada la matriz 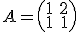
Calcula una matriz 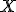 de forma que
de forma que 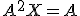
La matriz 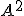 es
es
2 3
y la matriz 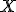 es
es
Aquí os presentamos un video donde se muestra los pasos a dar para la obtención de la inversa de una matriz.
Calcula dos números naturales  y
y 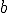 menores que 10 de forma que la matriz
menores que 10 de forma que la matriz 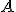 tenga rango 2, siendo
tenga rango 2, siendo
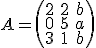
Calcula el rango de la matriz 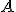 en función del parámentro
en función del parámentro 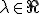 , siendo
, siendo 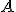 la siguiente matriz:
la siguiente matriz:
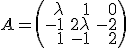
Estudia el rango de la matriz 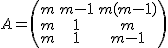
Determina el rango de la matriz 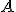 en función de los valores del parámetro
en función de los valores del parámetro 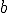
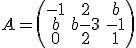
Si 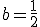 el rango es
el rango es
Si 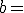 el rango es
.
el rango es
.
En caso contrario el rango es
En el enlace a la siguiente página puedes encontrar videos en donde se muestra la resolución de ejercicios sobre matrices.
En concreto puedes fijarte en los siguientes ejercicios y explicaciones que aparecen en el enlace de arriba:
07. Suma de matrices equidimensionales.
08. Producto de un escalar por una matriz.
10. Producto de matrices.
11. Traspuesta de una matriz
15. Transformaciones elementales.
16. Determinante de una matriz cuadrada
17. Menor complementario. Cofactor o adjunto.
18. Desarrollo de los determinantes por los elementos de una línea.
20. Matriz adjunta de una matriz cuadrada.
21. Matriz inversa de una matriz cuadrada.
22. Submatrices y menores de una matriz.
23. Rango de una matriz.
25. Cálculo del rango.
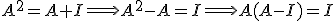
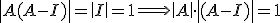
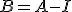 podría ser la inversa de la matriz
podría ser la inversa de la matriz 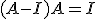 . Comprobémoslo:
. Comprobémoslo:
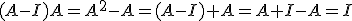
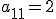 que no es cero, por lo que el rango de
que no es cero, por lo que el rango de 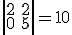
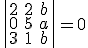
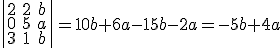
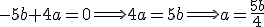
 es 10 que no es menor que 10.
es 10 que no es menor que 10.
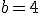 y, por tanto
y, por tanto 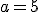 . Con estos valores, el rango de la matriz
. Con estos valores, el rango de la matriz