3.3. Paso de diédrico a Axonométrico
Para realizar un dibujo o perspectiva axonométrica podemos emplear las plantillas de dibujo o crear una retícula, llamada PAUTA AXONOMÉTRICA formada por las direcciones de los ejes axonométricos.
El origen de esta retícula es la pauta ortogonal, de estructura
cuadrangular, cuyas direcciones son las de las vistas diédricas del
objeto a representar.
Así pues, al pasar del sistema diédrico al axonométrico, el cuadrado se adapta a los ejes axonométricos, transformándose en otro cuadrilátero (rombo o romboide). Para realizar un dibujo o perspectiva axonométrica podemos emplear las plantillas de dibujo o crear una retícula, llamada PAUTA AXONOMÉTRICA formada por las direcciones de los ejes axonométricos.
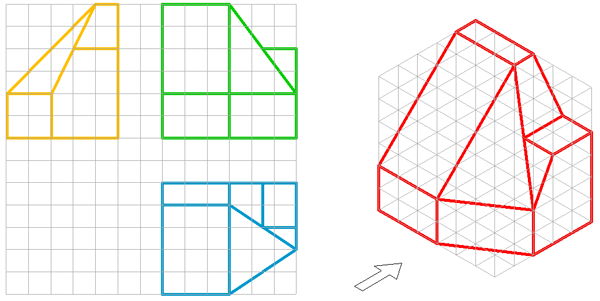
Cuando representamos piezas en perspectiva axonométrica, normalmente recurrimos a la isometría, ya que la disposición de sus ejes facilita el trazado, ya sea con las plantillas de dibujo (los ángulos del cartabón coinciden con los ejes isométricos) o mediante la PAUTA ISOMÉTRICA. En la imagen superior tienes un ejemplo de representación isométrica mediante el empleo de una pauta isométrica
- Axonometría ortogonal: se transforma en un ROMBO o ROMBOIDE. En la animación inferior puedes ver el dibujo isométrico de un cuadrado.
- Axonometría oblicua: se transforma en un CUADRADO y en dos ROMBOIDES. En la animación inferior puedes ver la perspectiva caballera de un cuadrado (coeficiente de reducción 1/2).
LA PAUTA ISOMÉTRICA:
Cuando pasamos de una retícula ortogonal (PAUTA DIÉDRICA) al sistema ISOMÉTRICO obtenemos una retícula formada a partir de rombos cuyos lados siguen las direcciones de los ejes, por tanto, la estructura de dicha pauta será triangular (triángulos equiláteros).
En la animación inferior puedes ver la estructura de dicha pauta y cómo quedan dispuesta en ella las vistas diédricas.
En la animación inferior puedes ver cómo se realiza un dibujo isométrico (sin coeficiente de reducción) de una pieza dadas sus vistas diédricas: alzado, planta y perfil derecho, sobre una pauta isométrica.
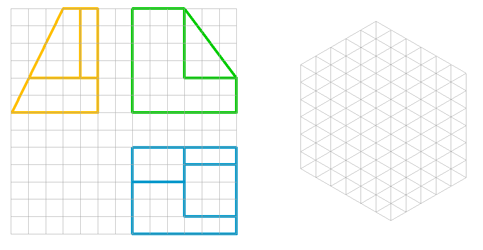 |
En la imagen izquierda tienes representada una pieza, según sus vistas
diédricas (planta, alzado y perfil derecho), sobre una pauta ortogonal;
tienes que realizar su dibujo isométrico sobre la pauta isométrica de
la derecha. |