3.2. Sistema de coordenadas
El triedro trirrectángulo de referencia, de vértice O. En la axonometría ortogonal divide al espacio en ocho triedros u octantes. Como origen de coordenadas tenemos al vértice O y las aristas OX, OY, OZ representan los ejes del sistema. Sus caras definen los planos coordenados o planos axonométricos: plano horizontal (XOY) y dos verticales (XOZ y ZOY). El primer triedro, zona ocupada por el observador, queda determinado por las direcciones positivas de las aristas, el resto queda conformado según se explica en a la siguiente animación:
Solamente vamos a representar, mediante coordenadas, los puntos situados en el primer diedro.
El sistema de coordenadas en Axonométrico que vamos a emplear es el mismo que usamos en el sistema diédrico, las coordenadas cartesianas (XYZ).
Podemos localizar cualquier punto, y definir su proyección directa, si describimos su posición con respecto a los tres ejes X,Y, Z .
- El origen: se sitúa en el vértice (O) del triedro. A partir de él el sentido puede ser positivo o negativo.
- El ancho: el eje X (coordenada desplazamiento) se extiende con su parte positiva hacia la derecha, a partir de O
- El alto: el eje Z (coordenada altura o cota), sentido positivo hacia arriba, a partir de O.
- La profundidad: eje Y (coordenada de alejamiento), sentido positivo hacia la derecha, a partir de O.
Representación de un punto por coordenadas.
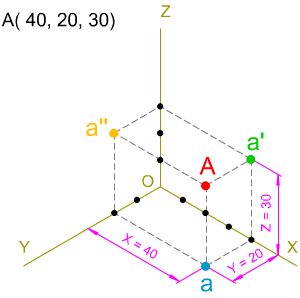
En la representación axonométrica, sin coeficiente de reducción, de un punto, dadas sus coordenadas, se sigue el procedimiento empleado en la imagen izquierda:
- Sobre cada eje axonométrico se coloca la coordenada correspondiente (sobre el eje X la coordenada X, etc.)
- Por cada punto determinado en un eje se trazan paralelas a los otros ejes (por la coordenada del eje X se dibujan paralelas a los ejes Z e Y).
- La intersección de dos paralelas determina la proyección secundaria del punto (paralelas a los ejes X y al Y determinan la proyección secundaria a).
- Las paralelas trazada desde las proyecciones secundarias (a cada eje restante) determinan en su intersección la proyección directa del punto (las paralelas dibujadas por las proyecciones secundarias a y a' (a los ejes Z e Y respectivamente) determinan la proyección directa A).
En la animación inferior puedes ver de manera detallada este procedimiento.
Necesitamos dos coordenadas, como mínimo, para poder definir la proyección secundaria de un punto.
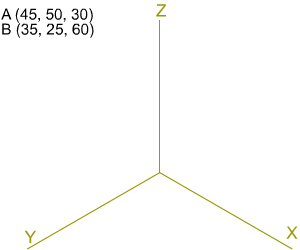 |
En la imagen izquierda tienes las coordenadas axonométricas de los
puntos A y B y los ejes isométricos X, Y, Z; tienes que dibujar las
proyecciones isométricas de los puntos dados y del segmento M que pasa
por dichos puntos. |