2. Contrastamos la proporción
 |
| Imagen de Patricio Campos bajo licencia Creative Commons |
Bueno, pues vamos a meternos ya en faena. Ya hemos visto todo lo necesario para resolver un problema usando un contraste de hipótesis, así que, vamos a aplicarlo y vamos a resolver estos problemas aplicando esta técnica.
Vamos a seguir las mismas pautas que has visto en los dos temas anteriores para los intervalos de confianza, es decir, vamos a resolver problemas relativos a la proporción de un carácter en una población, a la media de una población que sigue una distribución normal y a la diferencia de medias de poblaciones normales con desviaciones típicas conocidas.
Vamos a empezar entonces contrastando hipótesis sobre la proporción, pero antes de hacer nada, vamos a pensar en qué estadístico habrá que utilizar para realizar el contraste.
Si recuerdas, en el tema 4 de la unidad anterior, vimos que en una distribución binomial, la distribución en el muestreo del parámetro p si n era mayor o igual que 30 seguía una distribución normal:
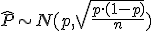
Claro, sabemos la distribución, una normal, pero esa distribución normal no es práctica ya que no sabemos las probabilidades sobre ella, pues las probabilidades de la Normal las sabemos calcular para la N(0,1). Pero bueno, eso nos es mucho problema ¿no? Basta con tipificar esa variable y nos quedaría así:
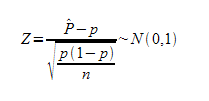
Así que, ese estadístico que sigue una distribución normal N(0,1), será el estadístico del contraste en cualquier contraste de hipótesis sobre la proporción en una población que siga una distribución binomial.
Si X es una variable aleatoria que sigue una distribución binomial B(n,p) y queremos contrastar una hipótesis sobre el parámetro p, el estadístico del contraste será:
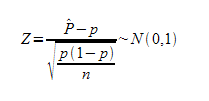
donde 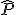 indica el valor muestral del parámetro o el valor de p obtenido en la muestra y p el valor teórico del mismo que se supone para toda la población.
indica el valor muestral del parámetro o el valor de p obtenido en la muestra y p el valor teórico del mismo que se supone para toda la población.
 |
| Imagen de acebal bajo licencia Creative Commons |
Me llamó la atención la noticia que leí en el periódico Diario de Sevilla el otro día, donde el titular afirmaba que uno de cada tres niños sufría sobrepeso. Leyendo la noticia un poco más, decía que aproximadamente cerca del 30% de los niños y niñas con edades comprendidas entre 3 y 12 años sufrían sobrepeso. ¿Será esto verdad?
Mi amiga Merce trabaja en el área de Sanidad del ayuntamiento, y al comentarle la noticia me dijo que iba a comprobar si en nuestro pueblo esto también era así de alarmante. Así, se puso en contacto con Tisbet Survey y les encargó que estudiaran el sobrepeso en la población infantil de la localidad. Fíjate que casualidad que en Tisbet Survey le comunicaron que ese trabajo estaba ya prácticamente hecho pues una empresa farmacéutica se lo había encargado no hacía mucho tiempo.
Tras el previo trabajo que ya conoces, de seleccionar adecuadamente la muestra, en Tisbet Survey realizaron 250 encuestas, o sea, analizaron el peso de 250 niños y niñas de la localidad en esa franja de edad y comprobaron que 53 sufrían sobrepeso. ¿Confirmarán en Tisbet Survey, que la proporción de sobrepeso en la localidad es efectivamente del 30%?
 |
| Imagen de Martin Catharae bajo licencia Creative Commons. |
Una marca de tomate frito, ha cambiado el diseño de su bote de 200 gramos con el fin de hacerla más atractiva al consumidor. Los publicistas creen que el nuevo formato tendrá una buena acogida y que alrededor de tres cuartas partes de los clientes están de acuerdo con su diseño.
Para dar crédito a tal afirmación preguntan a 50 consumidores de esa marca sobre la opinión sobre el nuevo formato y 39 se mostraron favorables. ¿Puede afirmarse con un 10% de significación entonces que la proporción de clientes satisfechos es esa?
La hipótesis nula es H0 : p = .
El nivel de significación es α =
La región crítica es ( -∞ , ) U ( , + ∞).
El valor de p en el muestreo es y por tanto el del estadístico del contraste en el muestreo es (usa 4 decimales)
Así pues, ¿acepto o rechazo la hipótesis nula?:
Para el contraste de hipótesis
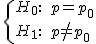 con un nivel de significación α, la región crítica o de rechazo viene dada por:
con un nivel de significación α, la región crítica o de rechazo viene dada por:
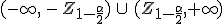
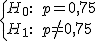 y el nivel de significación α = 0,1; por lo que
y el nivel de significación α = 0,1; por lo que 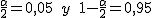
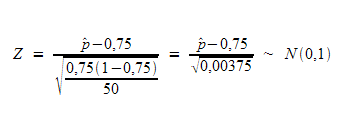
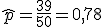 y por tanto nuestro valor muestral del estadístico es
y por tanto nuestro valor muestral del estadístico es 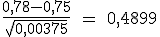 .
.