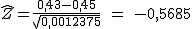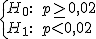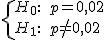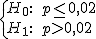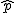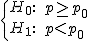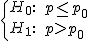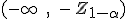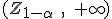2.1. Mayor o menor
 |
| Imagen de Keith Allison bajo licencia Creative Commons |
En el apartado anterior hemos visto cómo se hace un contraste de hipótesis para un valor concreto de una proporción, pero no siempre nos interesa saber si la proporción es un valor concreto, sino si supera un límite o es inferior a una determinada barrera. Por ejemplo, saber si los accidentes laborales han bajado de cierta proporción tras una campaña publicitaria de sensibilización, si la proporción de gente satisfecha con un producto ha aumentado de tal nivel, si la proporción de acierto del último fichaje del equipo de baloncesto es superior a la del jugador de la temporada pasada,...
En la gran mayoría de casos, son estos valores los que nos importan, y como vas a ver todo se hace prácticamente igual. Lo que varía es la región crítica que ahora, al ser contrastes unilaterales tendrán un solo intervalo, menores que un cierto valor o mayores que otro.
Como truco, puedes quedarte con la idea de que la desigualdad de la hipótesis alternativa es la que me da la forma del intervalo de la región crítica.
Si la hipótesis alternativa es p>p0, la región crítica será de la forma (k , +∞) y si la hipótesis alternativa es p<p0, la región crítica será (-∞, k) con k un número real.
 |
| Imagen de Symic bajo licencia Creative Commons |
Un sindicato de trabajadores observa con preocupación que muchas empresas, con la excusa de la crisis de ventas y apoyándose en el miedo del trabajador o la trabajadora en ser despedida, no paga las horas extras al precio estipulado en el convenio o ni siquiera las paga.
Desde el sindicato sostienen que al menos un 45% de los trabajadores no cobran correctamente las horas extras, pero para no lanzarse a la piscina al denunciar, deciden estudiar más afondo el asunto y contratan los servicios de Tisbet Survey para que analicen en profundidad esta cuestión.
En Tisbet Survey se centran en el ramo de la alimentación y analizan 200 trabajadores de distintas empresas. De estos doscientos trabajadores, 114 cobraron correctamente sus horas extras. Ante estos resultados ¿le dará la razón TisBet Survey al sindicato, suponiendo un nivel de significación del 3,5%?
 |
| Imagen de Felixe bajo licencia Creative Commons |
Una fábrica de piezas electrónicas asegura que, como máximo, un 2% de su producción es defectuosa. Analizadas 60 piezas, se observa que 4 son defectuosas. ¿Puede aceptarse la hipótesis del fabricante con un nivel de significación del 5%?
1) Si llamamos p a la proporción de piezas defectuosas, el contraste de hipótesis que hay que plantear para resolver esta cuestión es:
|
| |
|
| |
|
|
|
(-∞, -1,65)
| |
|
(-∞ , -1,96)
| |
|
(1,96 , +∞)
| |
|
(1,65 , +∞)
|
|
0,0667
| |
|
2,58
| |
|
1,893
| |
|
142,81
|
|
Aceptar H0
| |
|
Rechazar H0
|
Contrastes de hipótesis unilaterales para la proporción "p" de una distribución binomial con un nivel de significación α:
| Contraste |
|
|
| Región Crítica |
|
|
En el siguiente vídeo te mostramos lo útil que puede llegar a ser el uso de una hoja de cálculo. En particular, usamos la hoja de cálculo para resolver contrastes de hipótesis sobre la proporción como los que hemos hecho en este tema. Además, al final del vídeo te mostramos la importancia de elegir adecuadamente el nivel de significación y la relación que existe entre nivel de significación y tamaño de muestra.
Hemos usado la hoja de cálculo de la suite ofimática de libre distribución OpenOffice Calc. Si todavía no lo has hecho, te puedes descargar el paquete ofimático OpenOffice en este enlace.
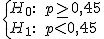
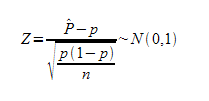
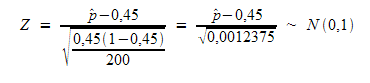
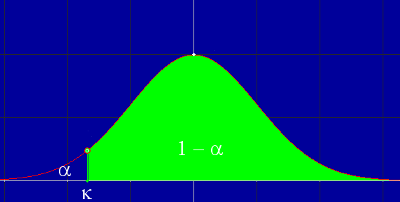 Fíjate que ahora rechazaremos la hipótesis nula si el valor obtenido es demasiado pequeño. Rechazar siendo cierta ocurrirá para valores muy pequeños y por tanto, la probabilidad α quedará en la cola de la izquierda de la normal N(0,1).
Fíjate que ahora rechazaremos la hipótesis nula si el valor obtenido es demasiado pequeño. Rechazar siendo cierta ocurrirá para valores muy pequeños y por tanto, la probabilidad α quedará en la cola de la izquierda de la normal N(0,1).
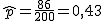 y entonces, nuestro estadístico en el muestreo vale
y entonces, nuestro estadístico en el muestreo vale