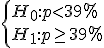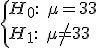1. Como Colombo
¿Te gustan las series de detectives? Hoy en día hay una multitud de ellas en nuestra televisión: CSI, El mentalista, Bones,...
En todas ellas, el buen detective analiza la escena del crimen o del delito, busca pistas, indicios, pregunta a testigos, investiga los negocios de la víctima, las relaciones familiares y sentimentales,..., en definitiva, va recopilando información para ir descartando posibles culpables hasta que todas las pistas centran las sospechas en una sola persona, ¡el asesino!
Antes de seguir, te ponemos un fragmento de una de las series míticas de detectives televisivos.
Bien, pues algo similar es lo que hacemos en Estadística, buscamos pistas e indicios en una muestra hasta que todas las evidencias nos indican lo que ocurre en la población, y para ello, para decidir adonde apuntan las pistas, usamos lo que en Inferencia Estadística se llama el Contraste de Hipótesis.
En los dos temas anteriores de la unidad, ya has visto que cuando en una población no conocemos algunos de los parámetros que identifican la distribución de probabilidad de la característica que estamos estudiando, una buena herramienta para estimar ese parámetro desconocido es el intervalo de confianza, esto es, un intervalo donde con una cierta probabilidad se encuentra el verdadero valor del parámetro. En este tema y el siguiente vamos a usar una nueva herramienta, el contraste de hipótesis. Básicamente se trata de plantear una hipótesis sobre el parámetro que se desconoce y a través de la muestra, decidir si tal hipótesis es cierta o no.
Importante
Un contraste de hipótesis es un procedimiento que nos permite decidir si una información sobre un parámetro de la población es aceptable o no a partir de la información obtenida de una muestra de esa población.
Por ejemplo, decidir si el peso medio de una población es 62 kg, la duración de unas bombillas es superior a 350 horas, o el precio medio de las latas de refresco en las tiendas de un barrio es inferior a 0,60 € son afirmaciones sobres parámetros desconocidos. Decidir si son aceptables esas afirmaciones se hará a partir de contrastes de hipótesis.
A la afirmación que se desea contrastar o comprobar su veracidad se le llama hipótesis nula, y se representa por H0. Frente a ella, se plantea siempre la hipótesis contraria que llamaremos hipótesis alternativa y representaremos por H1.
Ejemplo o ejercicio resuelto
 |
| Imagen de jesusbet bajo licencia Creative Commons |
La concejala de sanidad del ayuntamiento de Villalta, ante la preocupación del excesivo número de fumadores en la franja de edad entre 18 y 25 años, decide contratar a Tisbet Survey para que haga un estudio sobre los hábitos de los jóvenes de estas edades respecto a este asunto. Además, nuestra empresa farmacéutica también está interesada en este estudio para saber si pueden tener negocio vendiendo productos para dejar de fumar.
Tras un minucioso estudio mediante la realización de encuestas y observación directa, los estadísticos de Tisbet Survey llega a la conclusión de que la proporción de jóvenes fumadores asciende al 39%.
En vista de este alarmante resultado, se diseña desde la concejalía un programa de sensibilidad ante el tabaquismo que se espera reduzca este porcentaje de fumadores. Seis meses después, los trabajadores de Tisbet Survey vuelven a hacer el estudio. ¿Se habrá reducido el porcentaje de fumadores?
¿Cuáles son la hipótesis de este problema?
 |
| Imagen de leoncillo sabino bajo licencia Creative Commons |
Otro ejemplo, una máquina de envasado llena latas de refrescos y se sabe que la cantidad de refresco en cada lata sigue una distribución normal. El envasador asegura que la capacidad media de cada lata es de 33 cl, pero para comprobarlo, se toma una muestra de 50 latas. ¿Cuál sería el planteamiento del problema?
AV - Pregunta de Elección Múltiple|
H1: p ≠ 0,78
| |
|
H1: p < 0,78
| |
|
H1: p > 0,78
|
|
H1: A ≠ 10
| |
|
H1: A > 10
| |
|
H1: A < 10
|
Curiosidad
El nombre de "nula" indica que H0 representa la hipótesis que mantendremos a no ser que los datos indiquen su falsedad, y puede entenderse, por tanto, en el sentido de “neutra”.
Ojo, la hipótesis H0 nunca se considera probada, aunque puede ser rechazada por los datos. Por ejemplo, la hipótesis de que dos poblaciones tienen la misma media puede ser rechazada fácilmente cuando ambas difieren mucho, analizando muestras suficientemente grandes de ambas poblaciones, pero no puede ser probada la igualdad de dichas medias mediante muestreo, puesto que siempre cabe la posibilidad de que las medias difieran en una cantidad lo suficientemente pequeña para que no pueda ser detectada, aunque la muestra sea muy grande. O sea, con un contraste de hipótesis, más que un criterio para aceptar H0, lo que hacemos es crear un criterio para rechazar o no H0, es por eso que verás que en muchos ejercicios la respuesta final se da de la forma "Rechazo H0" o "No existen evidencias para rechazar H0".
 |
| Imagen de viZZZual.com bajo licencia Creative Commons |
Y ahora dirás, "Vale, todo eso está muy bien, pero, ¿cómo tomo la decisión?"
Bueno, todavía nos falta un poco para responder, pero imagino, que ya te habrás dado cuenta que la respuesta está en lo que diga la muestra que recojamos. Sobre esa muestra calculamos el valor del parámetro respecto al que estamos haciendo el contraste de hipótesis y según lo que valga aceptaremos o rechazaremos la hipótesis nula.
Fíjate en el primer ejemplo que hemos planteado, hemos dicho que la hipótesis nula es p < 39. Tomaremos una muestra en la población y en ella habrá que calcular la proporción de fumadores. ¿Cuándo rechazaremos H0? Pues parece evidente que si esa proporción me sale mucho mayor que 39 rechazaré la hipótesis alternativa, ¿no? O sea, rechazaré H0 si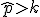 
, siendo 
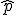la proporción obtenida en la muestra y "k" un valor que ya veremos más adelante como se obtiene.
Por tanto, se rechaza la hipótesis nula si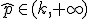 
.
En este caso decimos que el contraste de hipótesis es unilateral, pues la región en la que rechazamos la hipótesis nula consta de un solo intervalo; de una sola cola.
Fíjate ahora en el segundo ejemplo. La hipótesis nula plantea una igualdad frente a la alternativa de distinto de ese valor. ¿Cuándo rechazaremos ahora la hipótesis nula? Pues es lógico pensar en rechazar si la capacidad media de las latas de nuestra muestra difieren mucho de 33 cl, tanto por arriba como por abajo. O sea, si la media de las latas es mayor que un cierto valor o menor que otro cierto valor:
Rechazo H0 si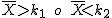 
O si lo expresamos con intervalos, rechazo H0 si :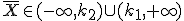 
Como ves, ahora la región de rechazo tiene dos zonas o intervalos. Es por esto que este contraste de hipótesis se llama bilateral.
Importante
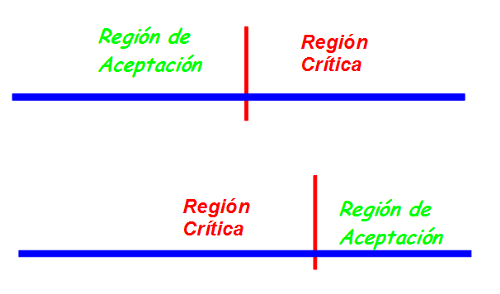
Los contrastes de hipótesis son de dos tipos según sea la región de rechazo o también llamada región crítica.
Si la hipótesis nula es de igualdad, el contraste de hipótesis se llama bilateral, pues la región crítica consta de dos partes.
Por contra, si la hipótesis nula plantea que un parámetro sea menor que un valor o mayor que un valor, el contraste se llama unilateral pues la región de rechazo consta de un solo intervalo. Así quedarían las regiones según la hipótesis nula sea de menor o de mayor que un cierto valor respectivamente:
AV - Reflexión