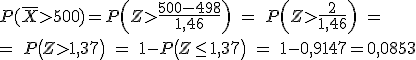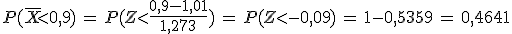2. La media de las medias

|
Cuando estamos haciendo un estudio sobre una población, por ejemplo, la satisfacción de los usuarios del metro de Sevilla valorados en una puntación entera de 0 a 100, lo que solemos hacer es escoger una muestra de 30 personas, por ejemplo, y reducir el estudio a esa muestra.
Pero si para esa muestra calculamos su media 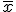 y su desviación típica s, obtendremos dos valores que pueden estar o no estar próximos a los valores de la media μ y de la desviación típica σ de la población, pues lo hemos hecho sólo para una muestra. Si repetimos el proceso sucesivamente con más muestras, lo lógico es que obtengamos valores distintos para esa media y esa desviación típica, ¿verdad?:
y su desviación típica s, obtendremos dos valores que pueden estar o no estar próximos a los valores de la media μ y de la desviación típica σ de la población, pues lo hemos hecho sólo para una muestra. Si repetimos el proceso sucesivamente con más muestras, lo lógico es que obtengamos valores distintos para esa media y esa desviación típica, ¿verdad?:
Muestra 1: 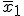 y s1
y s1
Muestra 2: 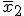 y s2
y s2
Muestra 3: 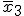 y s3
y s3
..........
¿Con cuál nos quedamos?
Los distintos valores de las medias de cada muestra 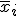 dan lugar a una nueva variable aleatoria, que por ejemplo, podemos representar así:
dan lugar a una nueva variable aleatoria, que por ejemplo, podemos representar así: 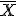 . La distribución de los valores de
. La distribución de los valores de 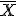 se llama distribución en el muestreo de la media.
se llama distribución en el muestreo de la media.
Esta nueva variable estadística, llamada Estadístico, tendrá su propia media 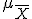 y su propia desviación típica
y su propia desviación típica 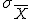 .
.
Veamos este vídeo del profesor de Bioestadística D. Francisco Javier Barón López de la Facultad de Medicina de la Universidad de Málaga que nos aclara bastante esta situación. Por cierto, las aplicaciones de las que habla al principio de vídeo serán las que veamos en la próxima unidad.
La distribución en el muestreo de la media 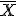 tiene las siguientes características:
tiene las siguientes características:
a. Media: Tiene la misma media que la población μ.
b. Desviación típica: La desviación típica de esta distribución es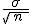 , siendo n el tamaño de las muestras.
, siendo n el tamaño de las muestras.
c. Si la población no sigue una distribución normal, pero n ≥ 30, la distribución de las medias muestrales se aproxima a una distribución normal, esta aproximación será mejor cuanto mayor sea n.
 |
| Imagen de guimoll con licencia
Creative Commons |
La empresa Sal Marina, S.A. comercializa sal que empaqueta en bolsas de 500 gramos. Se sabe que los pesos reales de las bolsas siguen una distribución normal de media 498 gr.y desviación típica 8 gr.
Si se toma al azar una muestra de 30 bolsas:
a) ¿Cuál es la distribución en el muestreo de la media?
b) Halla la probabilidad de que la media de la muestra sea mayor de 500 gr.
La misma empresa empaqueta también bolsas de 1 kilo, aunque la realidad marca que el peso medio de esas bolsas es 1,01 kg y la desviación típica 9 gramos.
Si sacamos una muestra de 50 bolsas de sal de un kilo, su peso medio expresado en kilogramos se distribuye según una normal N( ; ) (usa tres decimales para la desviación típica).
Además, en esa muestra, la probabilidad de que el peso medio sea menor que 900 gramos es .
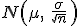 . En concreto:
. En concreto:
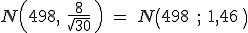
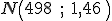 , vamos a calcular su valor tipificando la variable:
, vamos a calcular su valor tipificando la variable: