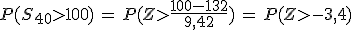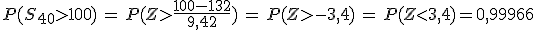3. Lo que todo lo justifica
 |
| Imagen de kadluba bajo licencia Creative Commons |
¿Ya te has familiarizado con esto de las distribuciones muestrales?
Parece todo un poco extraño, ¿verdad? Una distribución dentro de otra, un parámetro se convierte en variable, la media de las medias,... Uff, ¡qué lío!
Bueno, no tanto es así, y es que como te puedes imaginar, esto no sale de la chistera de un mago cual conejo saltarín, sino que todo tiene un fundamento, y eso precisamente es lo que vamos a ver en este apartado, aunque ya algo te han adelantado en el vídeo del apartado 2.
Lo que acabas de ver en los apartados anteriores de este tema es importantísimo, pues ten en cuenta que la distribución de la variable X se asocia a toda la población y conocer una característica de toda la población es complicado. De muestras no hay excesivos problemas, pero de toda la población... Pues bien, en la siguiente unidad, vamos a ver cómo se hace el salto de pasar la información de una muestra a toda la población, pero para ello son esenciales los resultados que acabas de ver.
De momento, sabemos la distribución que sigue la muestra (la media, la suma o diferencia de medias o la proporción) a partir de la distribución de la población, y en la próxima unidad, utilizando lo que acabamos de estudiar en estos apartados, veremos el paso contrario, que es lo verdaderamente interesante.
Por cierto, ¿no te ha resultado curioso que todo se aproxime a una normal? Sí, otra vez la distribución normal.
Como vamos a ver en el siguiente teorema, bajo ciertas condiciones, las cosas pueden parecerse mucho a una normal, y como recordarás, calcular probabilidades en una normal era bastante fácil.
¡Ah! este teorema es uno de los más importantes, o el que más quizás, de la estadística y la probabilidad, y todavía no lo hemos dicho, pero se llama Teorema Central del Límite.
El Teorema Central del Límite nos indica que si tenemos una serie de variables aleatoria independientes (el valor de una no influye en la otra) e idénticamente distribuidas (todas las variables tienen la misma distribución y por tanto, los mismos parámetros), la distribución de la suma de esas variables (si el número de variables que se suman es suficientemente grande) se aproxima a una Distribución Normal.
Lo precisamos todavía más, porque no se aproxima a una normal cualquiera sino que podemos saber a cuál:
Si tenemos n variables aleatorias X1, X2, X3,...,
Xn todas ellas independientes entre sí y todas ellas con
media µ y desviación típica σ, la suma de esas variables genera una
nueva variable aleatoria que se aproximará a una distribución Normal de
media 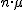 y desviación típica
y desviación típica 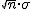
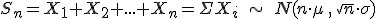
La coletilla de si el número es suficientemente grande no es ninguna tontería, pues lo que en realidad se aproxima es el límite de la suma de las variables cuando el número de variables tiende a infinito. O sea, que para que esto funcione, el número de variables o de datos que se han de sumar tiene que ser grande. A efectos prácticos nos vale con que al menos haya 30 datos, es decir, para aplicar este teorema tiene que cumplirse que n ≥ 30.
Ojo, fíjate que en ningún momento estamos diciendo que la variable X tenga que ser una distribución normal, sino que sea lo que sea la distribución de la variable en la población, la suma de muchas observaciones se va a aproximar a una normal.
Si ya de por sí la población de partida sigue una distribución normal, ese resultado se cumple siempre, sea el tamaño el que sea. No importa el valor de n.
|
N(12 ; 40)
| |
|
N(240; 28,28)
| |
|
N(240; 40)
| |
|
No se puede determinar.
|
|
N(5 ; 0,8)
| |
|
N( 150 ; 26,8)
| |
|
N( 150; 24)
| |
|
No puede determinarse.
|
 |
| Imagen de FreeCat bajo licencia Creative Commons |
|
N(197 ; 489)
| |
|
N(2364 ; 166,3)
| |
|
N(2364 ; 576)
| |
|
No se puede determinar.
|
 |
| PL Chebishev. Imagen en Wikimedia Commons bajo licencia Creative Commons |
Como ya sabes, la distribución normal tuvo su precedente en la binomial que Bernouilli desarrolló es su conocido Teorema Áureo, una función que años más tarde Poisson bautizaría como Ley de los Grandes Números. En 1733, el matemático francés De Moivre hizo una generalización de dicho teorema. No sólo fue el primero en obtener la característica forma de campana de la función, sino que también conjeturó, en 1733, el Teorema Central del Límite. Éste fue un resultado que, a pesar de no haber sido demostrado de forma rigurosa, fue aceptado durante mucho tiempo.
Una primera formulación clara del teorema no apareció hasta 1812, fecha en que Laplace llevó a cabo los primeros intentos de demostración. Aunque realmente el primero en iniciar un estudio riguroso fue el matemático ruso P. L. Chebyshev, siendo sus alumnos Markov, y especialmente Lyapunov, quienes resolvieron la cuestión de manera definitiva en 1901. Aunque la demostración completa del enunciado, tal y como lo conocemos actualmente, vino de la mano del matemático finlandés Jarl Waldemar Lindeberg (1876-1932) en 1930. Dicho enunciado dice: “La suma de un gran número de variables aleatorias independientes sigue aproximadamente una distribución normal”.
Pocas conjeturas se han mantenido como ciertas durante tanto tiempo y con el absoluto beneplácito de la comunidad matemática como la del Teorema Central del Límite. Ello fue debido, por una parte, a que nadie dudaba de su veracidad, y por otra, a la enorme utilidad que representaba su afirmación. La mayoría de los fenómenos que se dan en la naturaleza y en las sociedades humanas siguen una distribución normal. Se aplica de la misma forma para establecer sondeos electorales o sondeos petrolíferos. La psicología se sustenta como ciencia gracias a las medidas que establece en torno a parámetros como determinadas percepciones sensoriales o cocientes intelectuales. Todas las teorías que se construyen en torno a dichos resultados se vendrían abajo si el Teorema Central del Límite no fuera cierto.
En los apartados anteriores has visto que la distribución de la media
muestral es 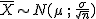 ¿Por qué es esto así? Pues fácil, a partir del
Teorema Central del Límite.
¿Por qué es esto así? Pues fácil, a partir del
Teorema Central del Límite.
Fíjate que acabamos de ver que la suma de las n variables, con las condiciones del Teorema, sigue una distribución Normal:
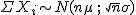
La media y la desviación típica de cualquier variable aleatoria cumplen que si la variable se multiplica por un número real, estos parámetros quedan también multiplicados por dicho número. Por ejemplo, imagina una variable aleatoria A que tenga de media 2 y desviación típica 0,4. La media de la variable aleatoria 3·A sería 3·2, o sea, 6, y la desviación típica 3·0,4 o lo que es lo mismo 1,2.
Bien, pues si recuerdas la fórmula de la media, ésta era 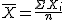 , es decir, la nueva variable ΣXi la
dividimos entre el tamaño de la muestra "n", o lo que es lo mismo, la
multiplicamos por
, es decir, la nueva variable ΣXi la
dividimos entre el tamaño de la muestra "n", o lo que es lo mismo, la
multiplicamos por 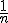 .
.
Si aplicamos la propiedad que acabamos de ver, la media muestral cumplirá que:
| Media | Desviación típica |
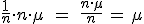 |
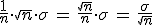 |
Luego efectivamente, se cumple que 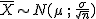 .
.
Las poblaciones normales
En el caso de que los datos vengan de una población normal, hemos dicho que es irrelevante el número de datos. No es necesario que haya 30 o más. Esto es debido a la propiedad reproductiva de la distribución Normal.
Esta propiedad nos dice que si hay dos variables aleatorias independientes que siguen distribuciones de probabilidad normales, la suma de ellas es también una distribución Normal con media la suma de las medias y varianza la suma de las varianzas.
Si suponemos que nuestra variable X~N(μ,σ), como cada Xi también tiene esa distribución, la suma de las n observaciones tendrá:
| Media | Varianza |
| μ+μ+...+μ = n·μ | σ2+σ2+...+σ2 = n·σ2 |
Y por tanto la desviación típica sería 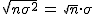 .
.
Es por esto entonces por lo que se cumple que 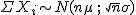 sea n el valor que sea y por tanto también,
sea n el valor que sea y por tanto también, 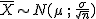 .
.
Esta propiedad de la reproductividad, es la que se utiliza para justificar también la distribución muestral de la suma de medias y diferencia de medias.
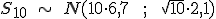 , o lo que es lo mismo,
, o lo que es lo mismo, 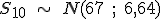

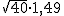 = 9,42
= 9,42