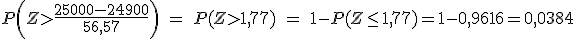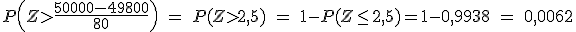2.1. Esperando en el médico
 |
| Imagen de medea_material con licencia Creative Commons |
Nuestra empresa TisBet Survey ha realizado un trabajo sobre el tiempo que duran las consultas de un determinado médico. Tras el estudio han concluido que las consultas duran una media de 8 minutos con una desviación típica de 2,3 minutos.
Supongamos que una mañana nuestro médico tiene 38 pacientes citados. ¿Cuál es la probabilidad de que termine antes de que transcurran 5 horas?
Fíjate que, a diferencia del apartado anterior, ahora no me piden la media de una consulta, sino que me están pidiendo cuánto duran de media las 38 consultas. Si tomamos una muestra de 38 personas y realizamos el experimento obtenemos:
1º La suma de todos los tiempos, que es t1. Por ejemplo t1=308 minutos.
2º Si repetimos el proceso obtendremos t1, t2, t3,... estos valores dan lugar a una nueva variable aleatoria T.
T es un estadístico cuyos valores siguen la distribución de las sumas muestrales de la variable "Tiempo medio de una consulta"
Importante
La variable aleatoria T tiene las siguientes características:
a. Media: n·μ, donde n es el número de individuos de la muestra.
b. Desviación típica :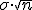 
c. Si la población no sigue una distribución normal, pero n ≥ 30, la
distribución de T se aproxima a una normal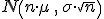 
.
En nuestro ejemplo, T="Tiempo que tarda en atender a 38 pacientes" sigue una distribución normal:
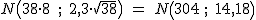
Por lo tanto, nos están pidiendo la probabilidad de que T<300. Calculémosla, tipificando la variable T.
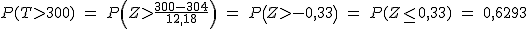
Podemos llegar a la conclusión que 6 de cada 10 veces ocurrirá esto, es decir, la consulta tardará más de 5 horas.
AV - Reflexión
 |
| Imagen de marcelo träsel con
licencia Creative Commons |
Recuerdas nuestro ejemplo de la empresa Sal Marina, S.A. del punto anterior:
La empresa Sal Marina, S.A. comercializa sal que empaqueta en bolsas de 500 gramos. Se sabe que los pesos reales de las bolsas siguen una distribución normal de media 498 gr.y desviación típica 8 gr.
Si las bolsas de 500 gr. se empaquetan en cajas de 50 y 100 unidades.
a) ¿Qué distribución siguen los pesos de las cajas de 50 unidades?
b) ¿Qué distribución siguen los pesos de las cajas de 100 unidades?
c) Si se coge al azar una caja de 50 unidades, ¿cuál es la probabilidad de que el peso de las 50 bolsas de sal supere los 25 kg.?
d) Si se coge al azar una caja de 100 unidades, ¿cuál es la probabilidad de que el peso de las 100 bolsas sea mayor de 50 kg.?
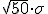. Si llamamos T50 a la variable de la suma
de los pesos medios de 50 bolsas de sal, esta variable sigue una
distribución normal N( 24900 ; 56,57).
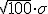. Si llamamos T100 a la variable de la
suma de los pesos medios de 100 bolsas de sal, esta variable sigue una
distribución normal N( 49800, 80).
