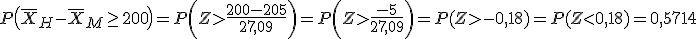2.2. Ahorremos energía
 |
| Imagen de Anton Fomkin con licencia Creative Commons |
Vemos la importancia que tiene el cálculo de la distribución de las medias. Pero aún hay más.
Veamos ahora un ejemplo que nos va a permitir comparar dos tipos de bombillas de bajo consumo de distintas marcas, pero de similares características.
Las bombillas de la marca A tienen una vida media de 11000 horas y una desviación típica de 1500 horas, mientras que las bombillas de la marca B tienen una vida media de 10000 horas y una desviación típica de 750 horas.
Supongamos que nos piden comparar las dos marcas. Cuál es la probabilidad de que una bombilla de la marca A dure mil horas más que una bombilla de la marca B.
Sean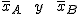 
sus respectivas medias muestrales.
Para comparar las dos marcas se considera la diferencia de sus medias,
que se estima con la diferencia de las medias muestrales: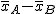 
Si se realiza este mismo proceso para otras muestras formadas por nA bombillas de la marca A y nB bombillas de la marca B. Se irán obteniendo sus respectivas diferencias de las medias:
, 
, 
, ....
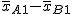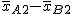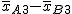Estos distintos valores dan lugar a una variable aleatoria que se
representa por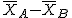 
.
La distribución de los valores de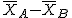
se llama distribución en el muestreo de la diferencia de las medias.
Importante
La distribución en el muestreo de la diferencia de las medias 
tiene las siguientes características:
a. Media: La media de la distribución es la diferencia de medias:
b. Desviación típica: La desviación típica es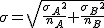 
c. Si la población no sigue una distribución normal, pero nA ≥ 30 y nB ≥30, la
distribución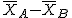
se aproxima a una normal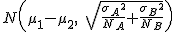 
Ejemplo o ejercicio resuelto
 |
| Imagen de reillybutler con licencia Creative Commons |
Vamos a resolver el problema con el que habíamos comenzado este apartado.
Supongamos que cogemos muestras de 50 bombillas de cada tipo.
La variable estadíastica
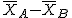sigue una distribución N(1000 ; 237,17), pues la diferencia entre las medias de A y B es 1000 y la desviación típica aplicando la fórmula sería:
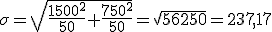
Para calcular la probabilidad de que una bombilla de la marca A dure
1000 horas más que una bombilla de la marca B sólo tendremos que
calcular . Como sabemos que la variable tiene una distribución
normal, vamos a calcular su valor tipificando la variable:
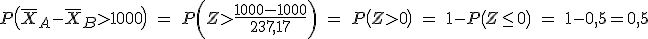
Es decir, una de cada dos bombillas de la clase A durará 1000 horas más que una del tipo B.
Si calculamos la probabilidad de que una de las bombillas de la marca B
dure más que una de la marca A, tendremos que calcular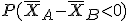 
Tipificando la variable tenemos:
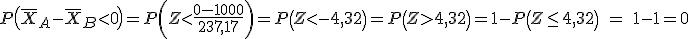
En conclusión, según el estudio que acabamos de hacer, una bombilla de la marca A durará más que una bombilla de la marca B.
AV - Reflexión
 |
| Imagen de amboo who? con licencia Creative Commons |
Una empresa ha contratado a TisBet Survey para que haga un estudio sobre la diferencia de los sueldos entre sus empleados. Están interesados en conocer si hay diferencia entre el salario medio de un hombre y de una mujer.
Para ello se han tomado una muestra aleatoria de 60 mujeres y de 40 hombres obteniendo los resultados que figuran en la tabla inferior:
| Hombres | Mujeres |
|
| Media |
1230 € |
1025 € |
| Desviación Típica |
160 € |
75 € |
Ayuda a nuestros amigos calculando la distribución en el muestreo de la diferencia de medias muestrales y la probabilidad de que la diferencia de las medias entre los salarios de los hombres y de las mujeres sea superior a 200 €.
.
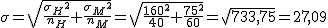
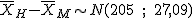
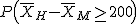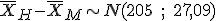, para calcular esta probabilidad tipificaremos la
variable y usaremos las tablas para ver su valor.
