1. ¿Cómo perder el miedo a volar?

|
| Imagen de Kevin bajo licencia Creative Commons |
Existen ocasiones en las cuales no estamos interesados en la media de la muestra, sino que queremos investigar en la muestra la proporción de artículos defectuosos, la proporción de alumnos suspendidos o la proporción de pacientes que con una terapia determinada pierden el miedo a volar, por poner algunos ejemplos.
Para dar respuesta a estas situaciones vamos a utilizar lo que llamamos distribución muestral de proporciones.
Si te acuerdas de la unidad anterior, cuando en una población estudiábamos una determinada característica o variable que sólo podía tomar dos valores, éxito o fracaso, la población seguía una distribución binomial.
En esta población, la proporción de individuos que poseen esa característica la llamamos p y en todas las muestras de tamaño n que podamos extraer de la población, llamaremos 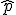 al porcentaje de individuos que tengan esa característica.
al porcentaje de individuos que tengan esa característica.
Los distintos valores de 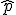 que dependen de las muestras elegidas, dan lugar a una variable aleatoria que se representa por
que dependen de las muestras elegidas, dan lugar a una variable aleatoria que se representa por 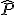 y que se llama estadístico.
y que se llama estadístico.
Llamamos distribución muestral de proporciones a la distribución de los valores de 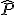 .
.
La variable aleatoria 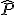 tiene las siguientes características:
tiene las siguientes características:
a) La media es: 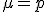 .
.
b) La desviación típica es: 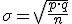 , siendo
, siendo 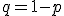 .
.
c) Para muestras donde n≥30, la distribución de 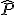 se aproxima a una distribución normal
se aproxima a una distribución normal 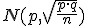 .
.
 |
| Imagen de jfgornet bajo licencia Creative Commons |
El profesor de Matemáticas lleva a la clase una bolsa con 4 tarjetas y en cada una de ellas aparece una cifra: 1, 2, 3, 5.
a) ¿Cuál es la proporción p de cifras pares?
b) Ahora vamos a coger dos tarjetas de las cuatro, pero cogemos una, la miramos y la volvemos a poner en la bolsa, es decir, estamos obteniendo muestras con reemplazamiento de tamaño dos. ¿Cuál será la proporción de cifras pares para cada una de las muestras?
c) Calcula la media y la desviación típica de la distribución muestral de proporciones.
En un test de 5 preguntas, la variable "número de aciertos" con probabilidad p=0,50 se distribuye de la siguiente forma:
| Xi | 0 | 1 |
2 |
3 |
4 |
5 |
| f(xi) | 0,031 |
0,156 |
0,312 |
0,312 |
0,156 |
0,031 |
Definimos la variable 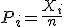 , "Proporción de aciertos con probabilidad p".
, "Proporción de aciertos con probabilidad p".
El estadístico proporción (P) se distribuye mediante el modelo Binomial: B(n,p).
La distribución de la proporción de aciertos queda de la siguiente forma:
| Xi | 0 | 1 |
2 |
3 |
4 |
5 |
| Pi | 0 | 0,20 |
0,40 |
0,60 |
0,80 |
1,00 |
| f(xi) | 0,031 |
0,156 |
0,312 |
0,312 |
0,156 |
0,031 |
Calcula:
a) La media y la desviación típica de P.
b) La probabilidad de que se acierten el 40% de las preguntas.
c) La probabilidad de que se acierten como máximo el 60% de las preguntas.
a) μ(p) =
σ(P) =
b) P(Pi = 0,40) =
c) P(Pi ≤ 0,60) =

|
| Imagen de wlappe bajo licencia Creative Commons |
La empresa TisBet Survey, le ha encargado a una imprenta que le haga tarjetas de visita.
Esta imprenta suele imprimir un 3% de tarjetas defectuosas.
Si han encargado 500 tarjetas:
a) ¿Cuál es la probabilidad de que reciban más del 5% de tarjetas defectuosas?
b) ¿Cuál es la probabilidad de que reciban menos de un 1% de tarjetas defectuosas?
El gerente de la empresa TisBet Survey tiene pánico a volar.
Le han recomendado a un psicólogo que afirma que con su terapia para tratar "el miedo a volar en avión" se recupera el 80% de los pacientes.
Si seleccionamos al azar a 50 pacientes que han acudido a su consulta durante los 6 últimos meses por este tema, ¿cuál es la probabilidad de que al menos el 75% se hayan recuperado y puedan tomar aviones?
La media de la distribución muestral de proporciones es 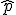 = μ(p) = p =
; y la desviación típica
= μ(p) = p =
; y la desviación típica
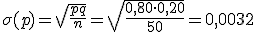 .
.
Como el tamaño de la muestra es superior a 30, la distribución muestral se distribuye según la normal . (Separa la media de la desviación típica con un ; y sin espacio)
La probabilidad que se pide es:
P(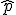 ≥
)=
- P(
≥
)=
- P(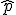 <
) = 1 -
<
) = 1 - 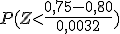 = 1 - P(Z<
) = 1-(1-P(Z<
))≈
.
= 1 - P(Z<
) = 1-(1-P(Z<
))≈
.
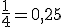 , ya que el único par es el número 2 de las cuatro cifras que tengo.
, ya que el único par es el número 2 de las cuatro cifras que tengo.
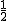 , pues de dos tarjetas, una es par.
, pues de dos tarjetas, una es par.
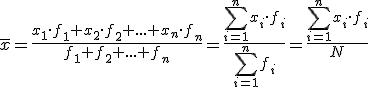
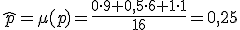
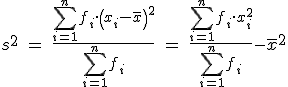
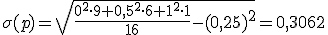
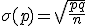 , siendo q=1-p=0,50.
, siendo q=1-p=0,50.
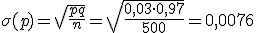
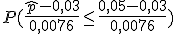 = 1 - P(Z ≤ 2,63) = 1-0,9957 = 0,0043.
= 1 - P(Z ≤ 2,63) = 1-0,9957 = 0,0043.
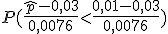 = P(Z< -2,63)= 1 - P(Z< 2,63)= 1 - 0,9957= 0,0043
= P(Z< -2,63)= 1 - P(Z< 2,63)= 1 - 0,9957= 0,0043