2. La curva de la hechicera

|
| Maria Gaetana Agnesi |
Se estaba haciendo tarde y Alba tenía que regresar a su casa. Aunque sabía que su amigo Martín tenía poco tiempo libre, quiso regalarle un bonito libro con la biografía de mujeres matemáticas a lo largo de la historia.
Martín le dio las gracias y esa misma noche empezó a leerlo.
Mirando el índice le llamó la atención un apartado que hablaba de una bruja y de una curva de una hechicera y se fue directamente a ese capítulo.
Se trataba de Maria Gaetana Agnesi, matemática, filósofa y lingüista, conocida popularmente por la curva de la hechicera.
La mal llamada curva de la hechicera la había estudiado previamente Fermat en 1703 y Grandi, en 1718, la bautizó con el nombre de versoria (en latín) o versiera (en italiano), refiriéndose al cabo que hace girar la vela de una nave.
Cuando Colson aprende italiano para traducir al inglés una obra tan importante, confundió versiera con avversiera (hechicera) y lo tradujo como witch of Agnesi (la bruja Agnesi) produciéndose la paradoja de que una mujer que dedicó su vida y su fortuna a los demás pase a la posteridad con el sobrenombre de bruja.
La curva de la hechicera es un caso particular de una función racional de segundo grado y como imagino irás intuyendo, en este tema estudiaremos las funciones racionales.
En la siguiente escena de GeoGebra creada por José María Vázquez de la Torre, si desplazas el punto B sobre la recta y=a (en este caso y=4), la trayectoria que dibuja el punto P es la representación de la curva de la hechicera.
Una función racional está
formada por un cociente de funciones polinómicas de la forma 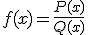 , donde Q(x)≠0.
, donde Q(x)≠0.
El dominio de una función racional está formado por el conjunto de todos los números reales menos aquellos valores de la x que anulan el denominador.
Asíntotas verticales: sus abscisas son los valores que anulan el denominador, es decir las raíces del polinomio Q(x).
Asíntota horizontal u oblicua
- Si grado de P(x) ≤ grado de Q(x), la recta y=k es una asíntota horizontal, donde
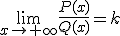 .
. - Si grado de P(x) = grado de Q(x) + 1, hay asíntota oblícua de la forma y=mx+n, donde mx+n es el cociente de la división entre P(x) y Q(x).
- Si grado de P(x) > grado de Q(x) + 1, entonces hay ramas parabólicas.
La curva de la hechicera tiene como expresión analítica 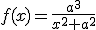 .
.
Analiza esta función racional para el valor a=2.
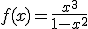
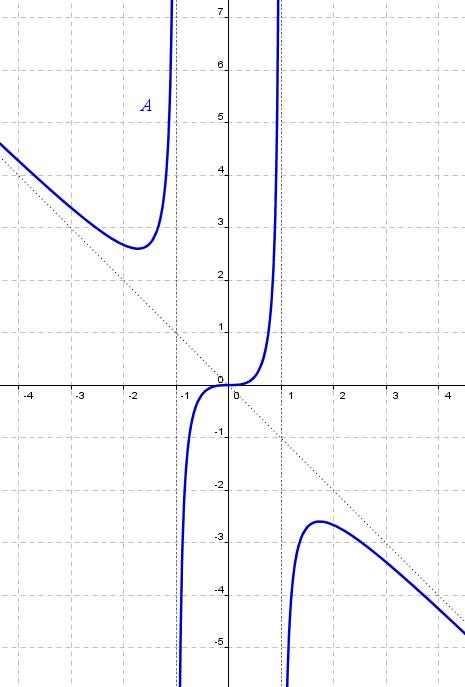
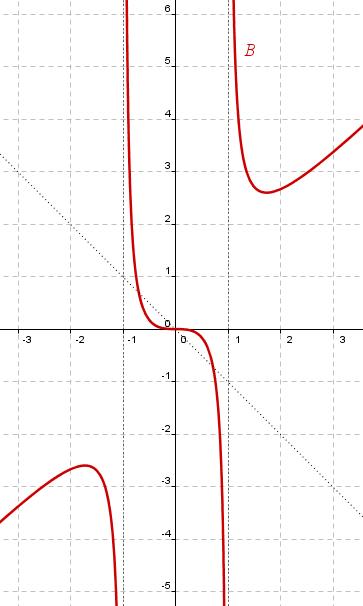
Previamente, completa los espacios en blanco y después señala cuál es la gráfica que le corresponde, A ó B.
1. Al ser una función racional es continua en todo R menos en los valores de x que anulan el denominador, que son x=
y x=
.
2. Como f(-x)=-f(x) es simétrica respecto del
.
3. Tiene dos asíntotas verticales en y .
4. Como el grado del numerador es igual al grado del denominador + 1, hay una asíntota oblicua cuya ecuación es .
5. La primera derivada de f(x), una vez simplificada es  .
.
Para calcular los máximos y mínimos, igualamos la primera derivada a cero. Como tengo un cociente, calculo los valores de x que anulan el numerador, que son x=
, x=- y x=
y x= .
.
6. La segunda derivada se anula en x=0, luego el punto (0,0) es un .
Para x=- la segunda derivada es positiva, luego el punto P=(-
la segunda derivada es positiva, luego el punto P=(- ,
,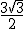 ) es un
.
) es un
.
Para x= la segunda derivada es negativa, luego el punto P=(
la segunda derivada es negativa, luego el punto P=( ,
, ) es un máximo.
) es un máximo.
7. El punto de corte con el eje Y es (
,
) y con el eje X (
,
) .
8. La gráfica de f(x) es
.
 |
 |
En esta página de Descartes creada por M.ª José García Cebrián, puedes analizar distintos tipos de funciones racionales.
a) Información extraída de la función
b) Información extraída de la derivada
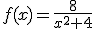 . Observo el denominador ya que en cada valor de x que anula el denominador tenemos una asíntota vertical y estos puntos no están en el dominio de la función.
. Observo el denominador ya que en cada valor de x que anula el denominador tenemos una asíntota vertical y estos puntos no están en el dominio de la función.
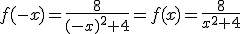

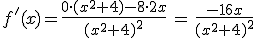

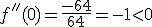
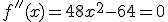 .
.
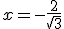 y en
y en  , luego tenemos dos puntos de inflexión en
, luego tenemos dos puntos de inflexión en  y en
y en 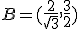 .
.