1. La Patrulla Águila
 |
El hecho de que actuara la Patrulla Águila, era un acontecimiento digno de ver, por eso Martín había llamado a su amiga Alba, la profesora de Matemáticas de la Universidad de Nogara.
Alba no faltó a la cita y fue acompañada de su hija pequeña María, ya que a ella le encantaban los aviones.
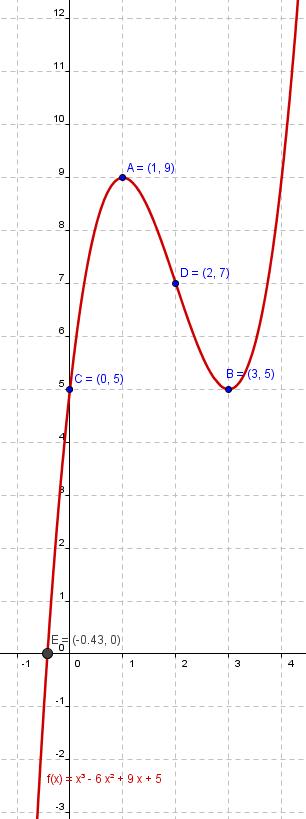
Cuando empezó la exhibición, a María se le escapó un precioso globo rojo que llevaba y empezó a llorar. Alba, su madre, enseguida la tranquilizó dándole un par de chucherías y mientras miraba como el globo se alejaba hacia el cielo se fijó en la forma de la cuerda del globo y le dijo a Martín que la cuerda estaba describiendo una gráfica de una función polinómica cuya ecuación se aproximaba a la de y=x3-6x2+9x+5.
Nuestro amigo Martín, al escuchar eso, lo primero que pensó es que Alba llevaba demasiado tiempo al Sol y no sabía lo que decía.
La verdad es que los matemáticos de vez en cuando dicen cada cosa.
En este apartado veremos cómo podemos identificar la gráfica de una función polinómica y representarla, utilizando todo lo que hasta ahora hemos estudiado.
¡Ánimo y a seguir trabajando!
A la hora de representar gráficamente una función tenemos que tener en cuenta que poseemos varios elementos que nos dan mucha información. A veces no necesitaremos utilizarlos todos, pero siempre nos ayudarán a realizar la gráfica de la forma más fiable.
Estos elementos son: dominio, recorrido, simetrías, asíntotas, máximos y mínimos, puntos de inflexión, puntos de corte con los ejes y otros puntos que puedan ayudarme a dibujar la gráfica.
Una función constante es una función polinómica de grado cero de la forma f(x)=a, cuya gráfica es una recta horizontal.
Una función lineal es una función polinómica de primer grado de
la forma f(x)=ax+b, cuya gráfica es una recta, donde a representa la pendiente de la recta y b la ordenada en el origen.
Una función cuadrática es una función polinómica de segundo grado de la forma y=ax2+bx+c, cuya gráfica es una parábola de eje vertical, donde a representa la abertura de la parábola.
Si a>0, la parábola está abierta hacia arriba y si a<0 la parábola está abierta hacia abajo.
Una función cúbica es una función polinómica de tercer grado de la forma f(x)=ax3+bx2+cx+d, con a≠0.
Corta al eje de abscisas en los puntos de la función cuyas primeras coordenadas son raíces del polinomio P(x)=ax3+bx2+cx+d, que se obtienen resolviendo la ecuación f(x)=0. Si las raíces son enteras, para encontrarlas se descompondrá el polinomio en factores utilizando el método de Ruffini.
Corta al eje de ordenadas en el punto (0,d).
Ejemplo: f(x)= -(x+1)·(x-1)·(x-2) = -x3 + 2x2 + x - 2.
Una función polinómica de grado n es de la forma y = a1xn+a2xn-1+ ... + an, con a1≠0.
Para calcular los puntos de corte de una función polinómica de grado mayor que 2 con el eje X, necesitamos recordar el método de Ruffini para factorizar un polinomio.
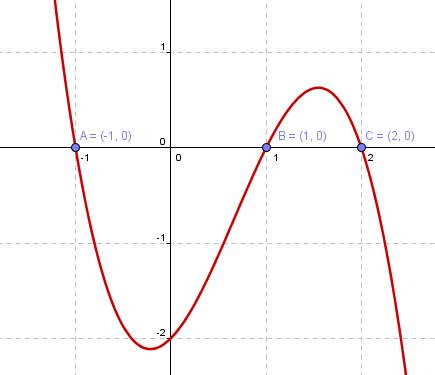
Representa la siguiente función: 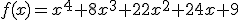 .
.
Previamente, completa los espacios en blanco y después señala cuál es la gráfica que le corresponde, A ó B.
1. Al ser una función es continua en todo R.
2. Cuando x tiende a -∞, la función tiende a ∞. Cuando x tiende a +∞, la función tiende a ∞.
3. La primera derivada de f(x) es f'(x)= x3+ x2+ x+ .
Para calcular los máximos y mínimos, igualamos la primera derivada a cero. Como tengo una ecuación de tercer grado, utilizo Ruffini, sabiendo que las soluciones son divisores de 24 (término independiente) y además son todas negativas, ya que todos los coeficientes de la ecuación son positivos.
También podemos probar, sustituyendo la x por -1, -2, -3, -4,-6,-12,-24.
Las soluciones son x=- , x=- , x=- .
El punto de corte con el eje Y es (0, ).
Si sabemos que corta al eje X en los puntos (-3,0) y (-1,0), la gráfica de f(x) es .
| A | B |
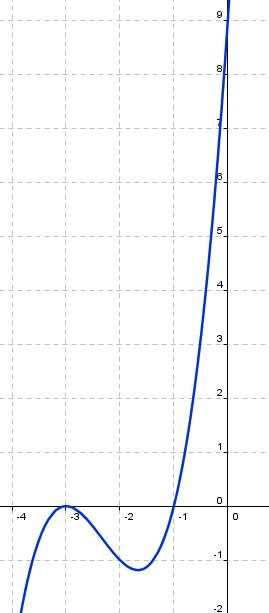 |
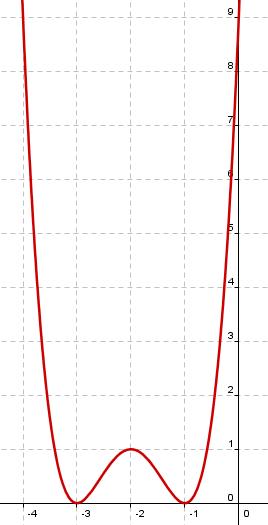 |
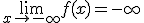 y
y 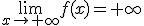 .
.
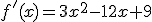
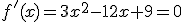
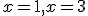 .
.
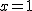 y a
y a 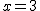 como candidatos a máximos y mínimos.
como candidatos a máximos y mínimos.
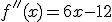 .
.
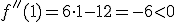
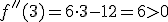
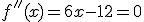 .
.