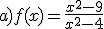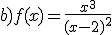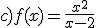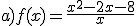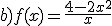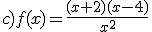2.1. El conjunto de Julia
 |
| Col fractal: Imagen de Efrén Sánchez bajo licencia Creative Commons |
Sonó el despertador y Martín dio un salto de la cama, cayéndose al suelo el libro que le había regalado su amiga Alba, ya que se había quedado dormido leyéndolo.
Mientras se lavaba la cara, recordó que después de haber leído a Gaetana Agnesi, le llamó la atención una fotografía que se parecía a una col que su amigo Felipe había encontrado el mes pasado en la finca "La Alfonsita" .
 |
| Mary Lucy Cartwright |
En el libro hablaban de un término muy raro que era la primera vez que él lo leía, algo así como "fractal" y de una matemática, Mary Lucy Cartwright, que con su “Teorema de Cartwright”, que trata sobre máximos de funciones, recurre a métodos que harán avanzar mucho su investigación sobre funciones y en especial sobre funciones que dan lugar a fractales.
Impresionado por este tema y deseoso de aprender, llamó a Alba y le preguntó que si tenía algún libro de fractales.
Alba le dijo que tenía varios y que le enviaría uno.
A la semana siguiente, cuando Martín recibió el libro, se detuvo en un tipo de fractal que se llama "Conjunto de Julia". Al principio creyó que Julia era una mujer, pero después leyendo el libro, se dio cuenta de que el fractal era de Gaston Maurice Julia, matemático francés precursor en lo que hoy se conoce como fractales.
Fue el primero en estudiar el tema y su notoriedad culminó al ser publicado su artículo informe sobre la iteración de las funciones racionales, galardonado por la Academia de las Ciencias Francesa.
Como te habrás dado cuenta, tienen mucha importancia las funciones que ahora estamos estudiando, las funciones racionales.
Si alguna vez habías oído hablar de fractales, seguramente habrías escuchado el conjunto de Maldebrot en vez de el de Julia, esto es debido a que Julia murió antes que se volvieran muy populares los fractales, a inicios de los años ochenta y el matemático también francés Benoit Mandelbrot, tuvo una ventaja enorme sobre Gaston Maurice Julia: pudo aprovechar la invención del ordenador.
A finales de los ochenta, los artistas se interesaron en el conjunto de Mandelbrot y en menor medida en los conjuntos de Julia, que están intrínsecamente relacionados.
En este apartado veremos distintas gráficas de funciones y las identificaremos con su expresión analítica (y=f(x)) correspondiente a una función racional.
 |
| Conjunto de Julia: Imagen de Wikimedia Commons bajo licencia Creative Commons |
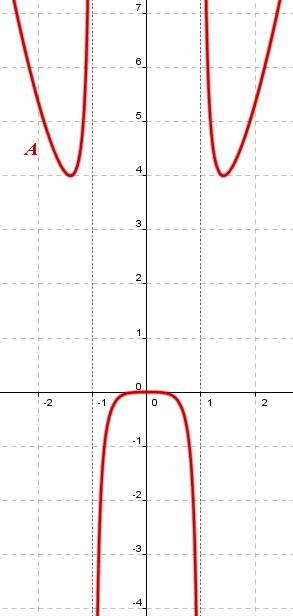
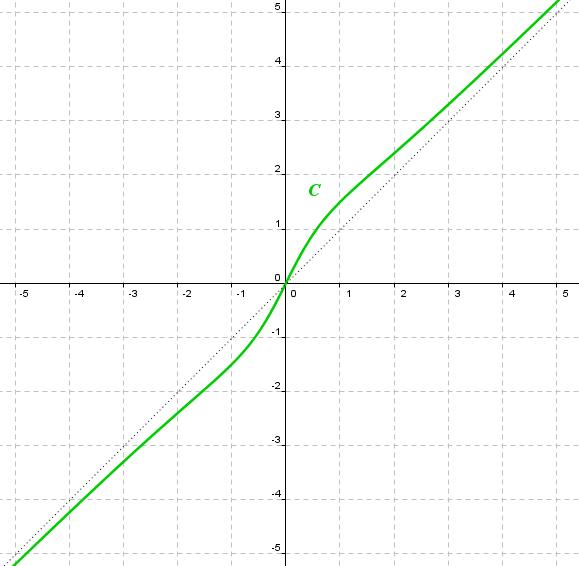
Identifica razonadamente cada una de las siguientes gráficas con su expresión analítica.
a) 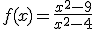 b)
b) 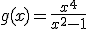 c)
c) 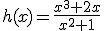
 |
 |
 |
Conoce un poco más del mundo apasionante de los fractales con estos vídeos.
En el primero puedes ver una entrevista muy interesante de Eduard Punset a Mandelbrot, en el segundo descubre los fractales en la naturaleza y por último prepárate para viajar al interior de una figura fractal.
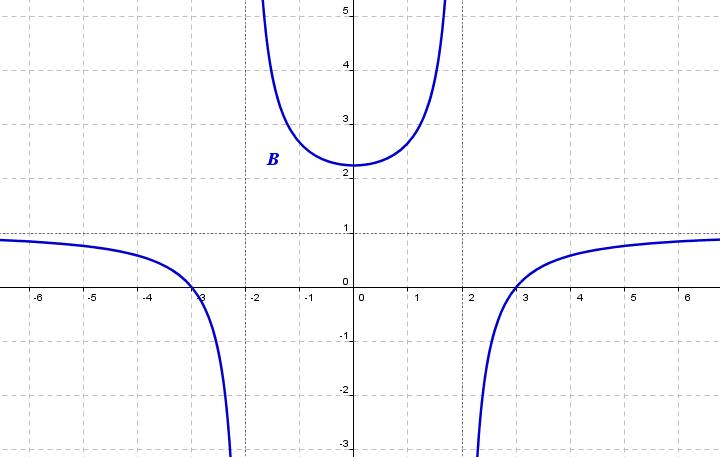
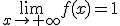 , y como vemos en la gráfica, hay una asíntota horizontal en y=1.
, y como vemos en la gráfica, hay una asíntota horizontal en y=1.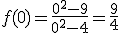 .
.
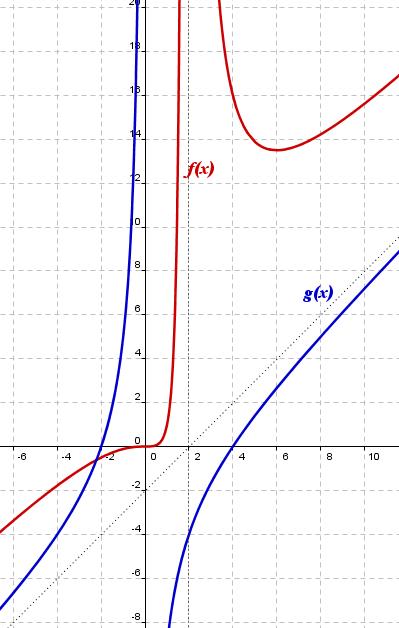 La expresión analítica de la gráfica de color rojo de la función f(x) es:
La expresión analítica de la gráfica de color rojo de la función f(x) es: