1.2. Vaya curvas
Para terminar de estudiar estas funciones que representan esa "belleza matemática", al menos para nuestra amiga Alba, como son las funciones polinómicas, vamos a ver cómo también nos ayudan a resolver problemas relacionados con la Geometría.
Problemas que aunque puedan parecer un poco complicados, si los analizamos y los vamos resolviendo poco a poco, nos producen una gran satisfacción cuando conseguimos resolverlos.
Antes de resolver ningún problema, te proponemos que busques fotografías donde puedas observar la representación de alguna función polinómica o bien una aproximación. Verás como te sorprendes.
 |
 |
 |
| Imagen de iakiskiss bajo licencia Creative Commons | Imagen de gonzalez-alba bajo licencia Creative Commons | Imagen de catikaoe bajo licencia Creative Commons |
Vamos a intentar el siguiente problema que le planteó un importante matemático inglés a nuestra amiga Alba cuando estuvo en Londres.
"Dado un cuadrado ABCD de lado 2 cm, consideramos la recta PQR perpendicular a la diagonal AC en el punto Q.
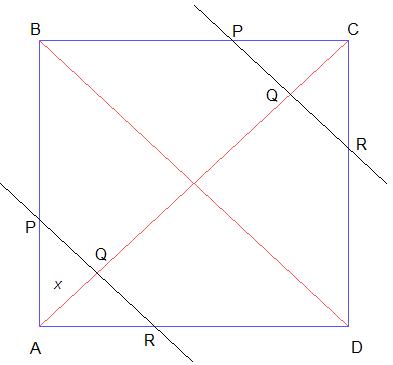
¿Qué expresión analítica corresponde a la función que da el área de la figura APR en función de la distancia AQ, siendo esta distancia mayor o igual que 0 y menor o igual que la longitud de la diagonal del cuadrado?
¿A qué tipo de función corresponde dicha expresión?
¿Cuál es el dominio de definición de la función que representa dicha área?
Representa gráficamente la función resultante.
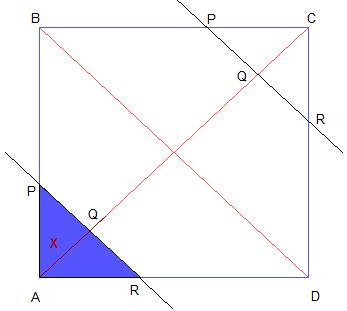
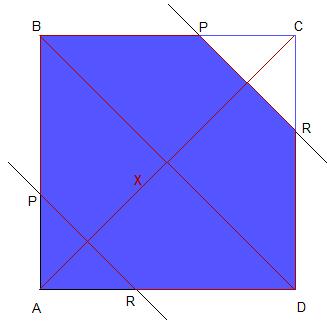
Observa el dibujo: la figura que se obtiene es un triángulo si AQ es menor (o igual) que la mitad de la diagonal AC o un pentágono ADRPB en otro caso."
 |
 |
| Triángulo |
Pentágono |
Solución:
Como el lado del cuadrado mide 2 cm su diagonal medirá 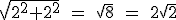 cm.
cm.
Para calcular la función área consideramos primero valores de la x, como ya hemos comentado, menores que la mitad de la diagonal, esto es, entre 0 y 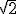 . En este caso, en los triángulos que se van formando, la
medida de PQ es igual a la de QR y esta igual a AQ=x ya que al ser PR paralela a la diagonal de un cuadrado los
triángulos APR son triángulos rectángulos isósceles.
. En este caso, en los triángulos que se van formando, la
medida de PQ es igual a la de QR y esta igual a AQ=x ya que al ser PR paralela a la diagonal de un cuadrado los
triángulos APR son triángulos rectángulos isósceles.
Por tanto, la base del triángulo es 2x y la altura x y entonces, el área del triángulo APR es 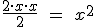 .
.
Para valores de la x entre 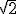 y
y 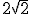 calculamos el área del
pentágono ADRPB restando al área del cuadrado el área del triángulo CPR.
calculamos el área del
pentágono ADRPB restando al área del cuadrado el área del triángulo CPR.
En ese triángulo, sigue siendo iguales las longitudes PQ, QR y CQ, pero ahora esta es la longitud dela diagonal menos la longitud de x, es decir, 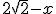 .
.
Así, el área del triángulo CPR es: 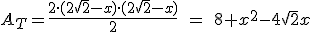
El área entonces del pentágono es:
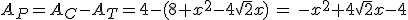
Como podemos apreciar, la función área está definida por dos expresiones dependiendo del valor
que tome la x entre 0 y 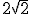 . Por tanto, tendremos una función definida a trozos cuyo
dominio de definición es el intervalo
. Por tanto, tendremos una función definida a trozos cuyo
dominio de definición es el intervalo 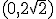
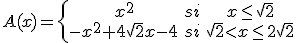
Para valores de la x entre 0
y 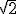 dibujamos una parábola
abierta hacia arriba (y=x2),
y para valores de la x entre
dibujamos una parábola
abierta hacia arriba (y=x2),
y para valores de la x entre 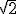 y
y 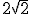 dibujamos una parábola
abierta hacia abajo con el vértice en el punto
dibujamos una parábola
abierta hacia abajo con el vértice en el punto 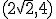
Su representación gráfica es:
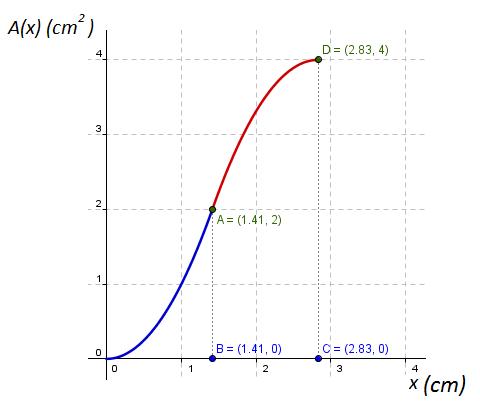
 donde la función cambia de curvatura, se denomina punto de inflexión.
donde la función cambia de curvatura, se denomina punto de inflexión.
(-2,0)
| |
(-1,0)
| |
(0,0)
| |
(1,0)
| |
(2,0)
| |
(3,0)
| |
(-2,0)
| |
(-1,0)
| |
(0,0)
| |
(1,0)
| |
(2,0)
| |
(3,0)
| |
(-2,0)
| |
(-1,0)
| |
(0,0)
| |
(1,0)
| |
(2,0)
| |
(3,0)
| |
(-2,0)
| |
(-1,0)
| |
(0,0)
| |
(1,0)
| |
(2,0)
| |
(3,0)
| |
El punto de corte con el eje Y de la función polinómica de tercer grado f(x) = x3-x2-x+1 es (0, ).
El punto de corte con el eje Y de la función polinómica de tercer grado g(x) = -x3+2x2+x-2 es (0, ).
El punto de corte con el eje Y de la función polinómica de tercer grado h(x) = -x3+x2+6x es (0, ).
El punto de corte con el eje Y de la función polinómica de tercer grado i(x) = x3+3x2+3x+1 es (0, ).
Dada la siguiente gráfica, relaciona cada función (A, B, C ó D) con su expresión analítica.
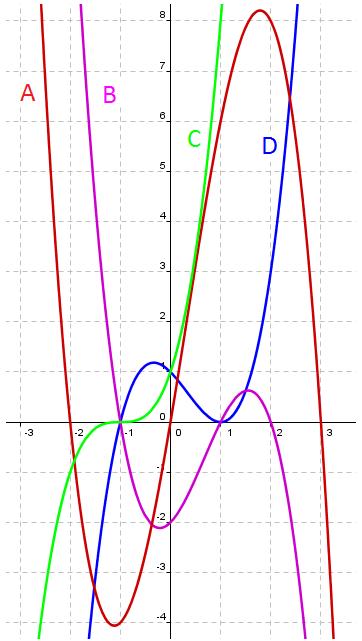
La gráfica de g(x) = -x3+2x2+x-2 es la que tiene la letra .
La gráfica de h(x) = -x3+x2+6x es la que tiene la letra .
La gráfica de i(x) = x3+3x2+3x+1 es la que tiene la letra .