1.1. Charles Babbage
 |
| Imagen de ricardo_ferreira bajo licencia Creative Commons |
Después de la magnífica exhibición aérea de la Patrulla Águila, Martín invitó a su amiga Alba a tomar un refresco en un quiosco que habían preparado los organizadores del evento.
Mientras tomaban el refresco acompañado de unas patatas fritas. Alba le contó a Martín que había estado durante el verano 15 días en Londres, gracias a una beca de la universidad y que uno de los sitios que le llamó mucho la atención fue el Museo de Ciencias.
Allí pudo ver la máquina que aparece en la imagen superior, la máquina diferencial de Babbage Nº 2.
Martín le preguntó que para qué servía un "cacharro" tan grande y Alba le dijo que era como una calculadora digital diseñada para tabular funciones polinómicas.
"Mira por donde, vuelven a aparecer estas funciones tan importantes que estamos estudiando".
En realidad, esta máquina lo que hace es calcular el valor numérico de una función polinómica obteniendo una tabla de valores que se aproxima a la función real.
Aunque esta máquina fue ideada por J. H. Mueller, Charles Babbage la redescubrió, aunque no llegó a construirla.
Una reconstrucción de esta máquina ha estado operativa desde 1991 en el Museo de Ciencia de Londres.
En este apartado veremos distintas gráficas de funciones y las identificaremos con su expresión analítica (y=f(x)) correspondiente a una función polinómica.
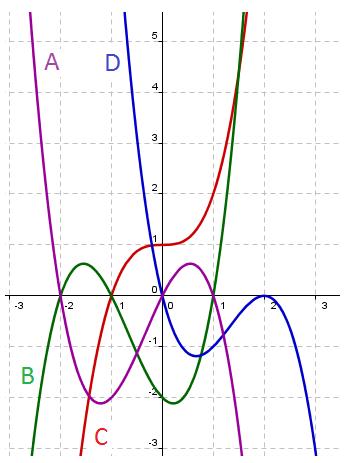 Identifica cada una de las siguientes gráficas con su expresión analítica.
Identifica cada una de las siguientes gráficas con su expresión analítica.Descubre la expresión analítica de aquella que no consigas identificar.
a) f(x) = x3 + 1
b) g(x) = x3 + 2x2 - x - 2
c) h(x)= -x3 + 4x2 - 4x
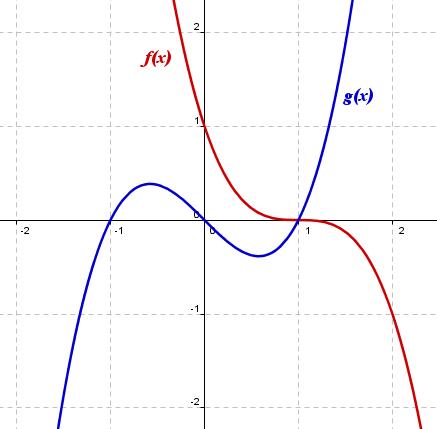 ión analítica correspondiente a la gráfica de f(x) de color rojo es:
ión analítica correspondiente a la gráfica de f(x) de color rojo es:
