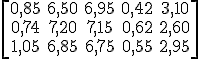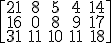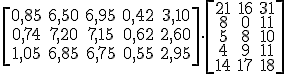3.3. Matriz x Matriz
|
| Imagen de DieselDemon bajo licencia Creative Commons. |
¿Y adivinas lo que viene ahora, no? claro, multiplicar una matriz por otra. Y es que la gran ventaja que nos aporta el uso de matrices es que podemos manejar simultáneamente un número elevado de datos.
En el ejemplo del apartado anterior hemos multiplicado un determinado número de productos por sus precios para determinar la ganancia, pero imagínate que estamos en una línea de montaje donde hay varios centros de producción y estos a su vez reciben materiales de diversos proveedores, y hay que tener en cuenta las horas de trabajo que tiene un producto en cada apartado de la línea de montaje, y después para deducir el beneficio, hay que ver los puntos en los que se venden los productos, y... y así todo lo que lo queramos enrevesar.
Todos estos pasos serían en la realidad multiplicaciones, y usando las matrices, éstas se pueden hacer de forma más rápida y sobre todo más ordenada. En el siguiente ejemplo te vamos a enseñar cómo se hace el producto de matrices (aunque en realidad ya casi sabes), y sobre todo, queremos que entiendas el porqué de hacer ese producto.
Ejemplo o ejercicio resuelto
 |
| Imagen de bpende bajo licencia Creative Commons. |
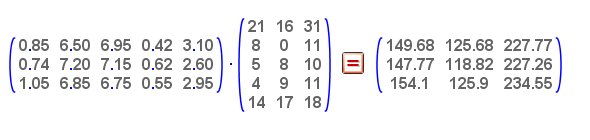
A Reme, una de las administrativas que trabaja en la oficina de TRANS VELOX de Morón y encargada de la compra del material de oficina, le han llegado tres catálogos de tiendas de material de oficina y decidida a ahorrar al máximo, decide hacer un estudio de precios concienzudo. Claro, como es normal, unas cosas están más baratas en una y otras cosas en otra, pero Reme quiere decidirse por un proveedor, así que como muestra, va a tomar los precios de cinco artículos en los tres proveedores y va a estimar el gasto que tendría siguiendo los pedidos del año pasado en el mismo mes.
Para el estudio, Reme ha observado el precio de las libretas, de las cajas de bolígrafos, de los recambios de los cartuchos de tinta, de las cajas de grapas y de los paquetes de folios.
En el primer proveedor, los precios son 0,85 € las libretas, 6,50 la caja de bolígrafos, 6,95 los cartuchos de tinta, 0,42 la caja de grapas y 3,10 el paquete de folio.
El segundo proveedor tiene los siguientes precios: 0,74 € las libretas, 7,20 los bolígrafos, 7,15 los cartuchos de tinta, 0,62 las grapas y 2,60 € el paquete de folios.
Por último, los precios que muestra el catálogo del tercer proveedor son: 1,05 € libretas, 6,85 bolígrafos, 6,75 € el cartucho de tinta, 0,55 la caja de grapas y 2,95 € el paquete de folios.
En cuanto a los pedidos, los realizados el año anterior en los meses de septiembre, octubre y noviembre fueron los que se reflejan en la tabla:
| Libretas |
Cajas de bolígrafos |
Cartuchos | Cajas de grapas |
Paquetes de folios |
|
| Septiembre |
21 | 8 |
5 |
4 |
14 |
| Octubre | 16 | 0 | 8 |
9 |
17 |
| Noviembre | 31 | 11 |
10 |
11 |
18 |
¿Qué decisión tomará Reme?
Importante
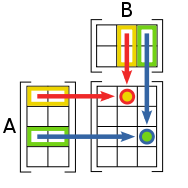
Para multiplicar dos matrices, tiene que cumplirse que el número de columnas de la primera matriz sea igual al número de fila de la segunda. Además, la matriz resultado tendrá el número de filas que tenga la primera matriz y el número de columnas de la segunda.
Anxp · Bpxq = Cnxq
Una consecuencia de esto es que el producto de matrices no es conmutativo, o sea, que A·B no tiene porqué ser igual que B·A. Es más a lo mejor ni siquiera se puede hacer B·A.
Si todavía no te ha quedado muy claro cómo multiplicar dos matrices, en los siguientes vídeos te lo explicamos paso a paso:
|
|
|
AV - Reflexión
Para saber más
Ahora en el producto, el elemento neutro es la matriz identidad del orden que le corresponde. Puedes comprobar que cualquier matriz por la identidad es ella misma.
A·I = A = I·A
Si quieres saber cuáles son las propiedades que cumple el producto de matrices sigue este enlace.
Curiosidad
 |
| Imagen de bibliotecapublicas.es bajo licencia Creative Commons |
¿Recuerdas los grafos del tema anterior? ¿Recuerdas que también se podían poner como matrices? Pues bien, el producto de matrices también se puede aplicar ahí, y más concretamente la potencia, o sea, multiplicar una matriz por sí misma una serie de veces.
Si A es la matriz de adyacencia de un grafo, A2 (A·A) representa el número de caminos que hay para ir de un lugar a otro en dos pasos, o sea, pasando antes por un lugar intermedio, A3 representaría el número de caminos que une los puntos dando tres pasos, A4 en cuatro pasos y así sucesivamente.
Vamos a verlo en un ejemplo. Recuerdas el mapa y el grafo que teníamos de los pueblos que rodeaban a Morón. Vamos a acortarlo un poco porque la matriz que salía era considerable. Vamos a quedarnos sólo con cuatro pueblos: Morón, El Coronil, Montellano y Coripe.
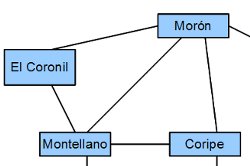
La matriz de adyacencia de ese grafo quedaría: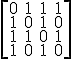 
colocando los pueblos en el orden anterior.
Si calculamos A2, obtendríamos lo siguiente:
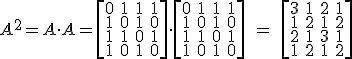
Por ejemplo, que a13=2 quiere decir que existen dos caminos para ir de Morón a Montellano en dos pasos, que serían ir de Morón a Coripe y de Coripe a Montellano y el otro ir de Morón a El Coronil y después de El Coronil a Montellano.