Imagen de zaturno bajo licencia Creative Commons.

¿Qué te parecería si te dijera que tu empresa va a duplicar la producción? Genial, ¿no? Doble de trabajo, doble de ventas, doble de ganancias,...

Pues nuestra empresa de transportes también ha conseguido doblar su facturación. Si recuerdas el ejemplo con el que empezamos el tema, estábamos analizando los repartos que había realizado TRANS VELOX durante la primera quincena de un mes en una de sus rutas. Teníamos que en la primera semana, transportaron 20 sobres o documentos, 48 paquetes de menos de 2 kg, 25 de entre 2 y 5 kg y 31 paquetes de más de 5 kilos. Y en la segunda semana los portes fueron 14 sobres, 50 paquetes de menos de 1 kg, 20 portes de entre 2 y 5 kg y 38 paquetes de más de 5 kg.

Matricialmente, habíamos escrito esos datos así: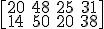  

Si decimos que en esa primera quincena del mes siguiente hemos doblado la facturación, esto querrá decir que de cada tipo de producto hemos facturado el doble, es decir, en la primera semana, en lugar de 20 sobres o documentos, habremos transportado 40, de paquetes de menos de 2 kg, en lugar de 48, llevaremos 96, de paquetes de entre 2 y 5 kilogramos, en lugar de 25, ahora serán 50, y así con todos. O sea, cada valor se multiplica por 2.

Está entendida la idea, ¿no? Bueno pues vamos a darle sentido a esto usando las matrices.