1. Cada ventana es un mundo y cada casa, más
 |
| Imagen de TwOse bajo licencia Creative Comm |
Antes que nada, vamos a recordar qué es una matriz, pues aunque ya lo hemos visto en el primer tema, no está de más volverlo a recordar para que nos quede bien clara la idea.
Como dijimos en el tema anterior, una matriz es un conjunto de números reales ordenados en filas y en columnas. Cada número o elemento de ese conjunto queda referenciado por la posición que ocupa, escribiéndose con subíndices el número de fila y de columna que ocupa.
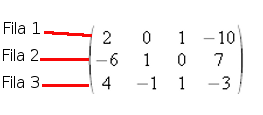
Si en la imagen quisiéramos llamar la atención sobre el balcón que tiene la toalla rosa, diríamos por ejemplo, que está en la segunda planta y en el segundo balcón de la derecha, ¿verdad? Pues con las matrices ocurre lo mismo, cada elemento es como si fuera un balcón de ese edificio y para llamarlo, se hace indicando la fila que ocupa y la columna, empezando la numeración de arriba abajo en las filas y de izquierda a derecha en las columnas:
 |
 |
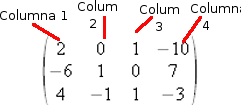Así por ejemplo, el elemento a21 es -6, pues es el valor del número que está en la fila 2 - columna 1, o el elemento a31 es 4.
Está claro, ¿no?
Ejemplo o ejercicio resuelto
 |
| Imagen de papersome bajo licencia Creative Commons. |
Ya en el tema anterior vimos como la información recogida en tablas se podía expresar mediante matrices. Vamos a ver que la información verbal también se puede adecuar a una matriz. ¿Recuerdas a nuestros amigos de TRANS VELOX? Pues, durante la primera quincena del mes, han seguido el número de portes que han hecho en una de las rutas y lo han clasificado en cuatro grupos, según el peso de los artículos transportados.
En la primera semana, transportaron 20 sobres o documentos, 48 paquetes de menos de 2 kg, 25 de entre 2 y 5 kg y 31 paquetes de más de 5 kilos. En la segunda semana los portes han sido 14 sobres, 50 paquetes de menos de 1 kg, 20 portes de entre 2 y 5 kg y 38 paquetes de más de 5 kg.
¿Podemos expresar esto como una matriz?
Importante
Una medida importante que hace referencia a matrices es la que se llama dimensión de la matriz.
La dimensión de una matriz indica el tamaño de la misma, es decir, el número de filas y columnas, y se expresa como m x n, siendo m el número de filas y n el de columnas.
En general, si la matriz es de la forma:
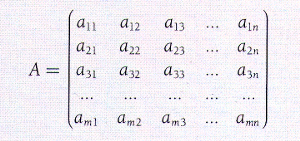
la dimensión es m x n.
Por ejemplo, en esta matriz, 
la dimensión es 3 x 4.
AV - Reflexión
 |
| Imagen de Sielarts informàtica bajo licencia Creative Commons. |
Antes de seguir, vamos a practicar un poco con lo que llevamos hasta ahora. Fíjate en la siguiente situación:
La empresa Infomax, monta ordenadores de mesa y portátiles. Para cada clase de ordenador la empresa dispone de tres tipos según la calidad y cantidad de sus componentes: alta media y baja.
En el mes de julio, montaron en ordenadores de mesa 20 de calidad alta, 40 de media y 40 de baja, mientras que en portátiles, montaron 32 de calidad alta, 28 de calidad media y 43 de calidad baja.
Por otro lado, en cada ordenador de mesa, se necesitan 4 horas de trabajo en el montaje y 6 en la instalación del software necesario, mientras portátiles, son necesarias 7 y 8 horas respectivamente. Pues bien, has de averiguar las matrices A y B que determinan el número de ordenadores según el tipo y la calidad y el número de horas de montaje e instalación con el tipo de ordenador respectivamente. Además, indica la dimensión de ambas matrices.
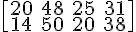
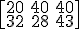y la dimensión sería 2 x 3.
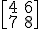y la dimensión sería 2 x 2.