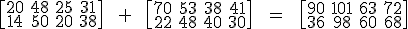2. Y empezamos a hacer cálculos
 |
| Imagen de Dicemanic bajo licencia Creative Commons. |
Esto de las matrices, como comprenderás, no sólo sirve para agrupar datos, sino que de forma cómoda nos permite hacer también muchas operaciones con esos datos. Sumar dos números no tiene ninguna complicación, sumar diez tampoco tiene mucha, pero sumar cien o quinientos o miles, ya hace que la cosa cambie.
Las matrices puesto que supone un ahorro en la ordenación de datos, nos van a servir también para que las operaciones que tengamos que hacer con ellos, las hagamos de una manera más cómoda y por tanto más rápida.
En este apartado vamos a comenzar a sumar y restar matrices y vas a ver que es lo más fácil del mundo.
Ejemplo o ejercicio resuelto
 |
| Imagen de Daquella manera. bajo licencia Creative Commons |
¿Recuerdas el ejemplo del primer apartado del tema?
Teníamos un cuadrante con los repartos que había hecho nuestra empresa de mensajería en la primera quincena de un mes en una de sus rutas de reparto. Esta tabla resume la información que teníamos:
| Ruta I |
Sobres | < 2 kg | Entre 2 y 5 kg |
> 5 kg |
| 1ª semana |
20 | 48 | 25 | 31 |
| 2ª semana |
14 | 50 | 20 | 38 |
y como matriz lo habíamos puesto así: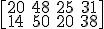 
Pero, ¿y si tuviéramos la información de otra ruta? ¿Cómo la juntaríamos?
Importante
La suma o resta de matrices se hace sumando o restando los elementos que están en las mismas posiciones, pero ojo, las dos matrices tienen que tener la misma dimensión. Además, la matriz solución sale también de la misma dimensión.
Apxq + Bpxq = Cpxq y cada elemento, cij = aij + bij
Imagino que te ha quedado claro, pero si no es así, observa este vídeo donde se explica paso a paso cómo hacer la suma de matrices:
AV - Pregunta de Elección Múltiple|
0
| |
|
Una matriz nula (todo 0) cuadrada de orden 2.
| |
|
Una matriz cuadrada de orden 4
| |
|
Una matriz cuadrada de orden 2
|
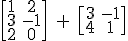es:
| |
| |
|
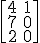
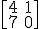
No se puede hacer esa suma.
|
|
Sí
| |
|
No
|
AV - Reflexión
 |
| Imagen de El Matenavegante bajo licencia Creative Commons |
Siguiendo el enlace puedes hacer ejercicios con sumas o restas de matrices. Haz al menos diez y asegúrate que te salen bien.
Para saber más
El elemento neutro de esta operación es la matriz nula (todos los elementos son ceros) de la misma dimensión que nuestra matriz A:
A + O = A
Si quieres ver las otras propiedades que tiene la suma de matrices, sigue el enlace.