3. ¿Alguna vez los conejos cubrirán toda la tierra?
¿Te has planteado alguna vez el número de seres humanos que habrá en la Tierra dentro de 1000 años? ¿Ó cuantos conejos habrá en el Parque de Doñana dentro de 150 años? Estos cálculos podemos realizarlos gracias a la dinámica de poblaciones, la cual nos indicará, dependiendo de la natalidad y mortalidad de los seres vivos estudiados el número de individuos dentro de x años.
Aquí tienes un vídeo donde puedes observar qué es la dinámica de poblaciones.
El tamaño de la población de los seres vivos se mantendrá alrededor de un valor fijo en función de la natalidad y mortalidad, las cuales vendrán dadas por dos funciones. Así, si partimos de una población inicial 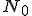 , con una tasa de natalidad de n (en tanto por uno), obtendremos una población en el primer año de
, con una tasa de natalidad de n (en tanto por uno), obtendremos una población en el primer año de 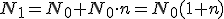 . De forma análoga podemos estudiar la mortalidad. Si la población tiene una tasa de mortalidad m, en el primer año morirán
. De forma análoga podemos estudiar la mortalidad. Si la población tiene una tasa de mortalidad m, en el primer año morirán 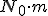 , por lo que la población tras el primer año, será
, por lo que la población tras el primer año, será 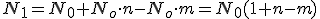 . Si llamamos r=n-m obtendremos la siguiente expresión
. Si llamamos r=n-m obtendremos la siguiente expresión 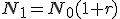 . Realizando las mismas operaciones para otros años llegamos a que en el segundo año
. Realizando las mismas operaciones para otros años llegamos a que en el segundo año 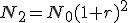 y para el año t, obtenemos
y para el año t, obtenemos 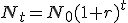 ¿Podemos asegurar que ocurrirá con esa población cuando el número de años que ha pasado es muy, muy grande? ¿Podemos calcular
¿Podemos asegurar que ocurrirá con esa población cuando el número de años que ha pasado es muy, muy grande? ¿Podemos calcular 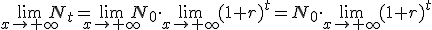 ?
?
El número r, puede aparecer también como una función dependiente de n, por lo que obtendríamos un límite con el siguiente aspecto 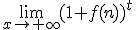 . El cálculo de este límite no es trivial, ya que dependerá de cada función. A los límites que no podemos asignar directamente su resultado, vamos a catalogarlos de una forma especial.
. El cálculo de este límite no es trivial, ya que dependerá de cada función. A los límites que no podemos asignar directamente su resultado, vamos a catalogarlos de una forma especial.
Llamaremos límite indeterminado ó indeterminación a aquellos límites en los que conocemos los límites de las funciones que intervienen, pero no podemos asignar el límite del resultado de la operación.
Las indeterminaciones más importantes son:
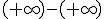 ,
, 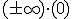 ,
, 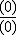 ,
, 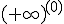 ,
, 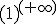 ,
, 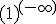 ,
, 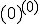 ,
,