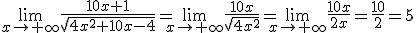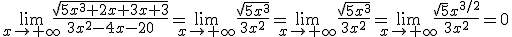3.2. La alimentación de los conejos.
 |
| Coneja. Banco de imágenes del ITE. Bajo licencia Cretive Commons. |
En una determinada zona de Andalucía, la población de conejos sigue una determinada función de crecimiento 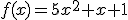 , donde x representa el número de años. Por otra parte, podemos estudiar el número de kg. de zanahorias producidos en la zona. La cantidad de kg. de zanahoria producida en el año x, viene dada por la función
, donde x representa el número de años. Por otra parte, podemos estudiar el número de kg. de zanahorias producidos en la zona. La cantidad de kg. de zanahoria producida en el año x, viene dada por la función 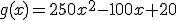 .
.
Si queremos saber la cantidad de comida que puede comer cada conejo basta dividir g(x) (cantidad total de comida) entre f(x) (cantidad total de conejos).
¿Pero, podemos indicar cuántos kg. de zanahoria comerá cada conejo al cabo de muchos, muchos años?
Para resolver una indeterminación donde intervengan fracciones algebraicas, debemos fijarnos en los exponentes de mayor grado de cada expresión algebraica
Sea 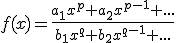 , entonces esta función tendrá en el infinito el mismo comportamiento que
, entonces esta función tendrá en el infinito el mismo comportamiento que 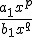
Así, si 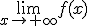
| p > q |
entonces
Si sg(a) |
| p = q | entonces 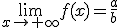 |
| p < q | entonces 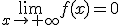 |
y si 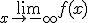
| p > q | Si p, q tienen igual paridad, entonces, si sg(a)=sg(b) 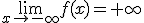 y y
si sg(a) |
Si p, q tienen distinta paridad, entonces si sg(a)=sg(b) , 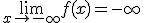 y y
Si sg(a) |
|
| p=q | entonces 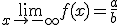 |
| p < q | entonces 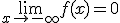 |
Calcula el siguiente límite: 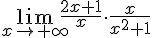
Determina el límite de las siguientes funciones:
1. 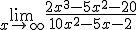
2. 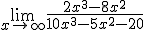
3. 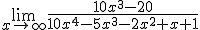
En los límites en los que aparezcan expresiones radicales, tendremos en cuenta las siguientes indicaciones.
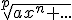 se comporta como
se comporta como 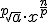
Calcula los siguientes límites cuando x tiende a + 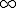
1. 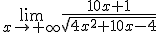
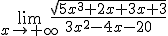
Calcula el siguiente límite: 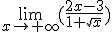
|
0
| |
|
1
| |
|
-3
| |
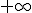
|
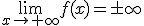 (Si sg(a)=sg(b) entonces
(Si sg(a)=sg(b) entonces 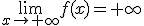 .
.
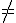 sg(b)
sg(b) 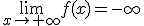 )
)
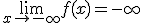
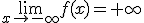
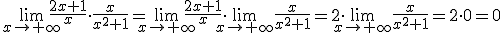
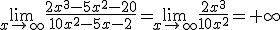
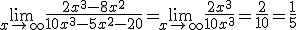
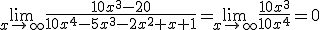
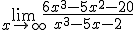

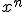 es 1
es 1