2.2. ¿Quieres ser millonario?
 |
|
Billete de 100 euros. Imagen tomada del Banco de recursos del ITE,bajo licencia Creative Commons. |
¿Quieres ser millonario? Eso nos preguntaban en un programa de televisión donde debíamos contestar 15 preguntas para conseguir 50 millones de las antiguas pesetas, pero ¿pueden las matemáticas ayudarte para ser millonario?
El interés compuesto consiste en invertir una cantidad de dinero a un determinado interés. Al acabar el año de inversión, invertimos el capital inicial, más sus intereses y así actuamos cada año.
Por ejemplo, si invertimos 10.000 € al 6 % anual.
Al finalizar el primer año obtenemos 10.000 x (1 + 0.06) = 10.600 y al finalizar el segundo 10.600 x (1 + 0.06) = 11.236
La expresión que nos da el capital obtenido al cabo de t años es
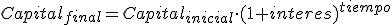
Veamos una tabla con el capital que podemos retirar al cabo de unos años
| Años | Capital en € |
| 0 | 10.000,00 € |
| 1 | 10.600,00 € |
| 2 | 11.236,00 € |
| 10 | 17.908,48 € |
| 20 | 32.071,35 € |
| 50 | 184.201,54 € |
| 100 | 3.393.020,84 € |
| 150 | 62.499.967,24 € |
| 300 | 390.624.590.520,47 € |
¡ Al cabo de 100 años tendremos 3 millones de euros ! ¡ Y tras 150 años, nuestros nietos tendrán 62 millones de euros! Al pasar años y años el capital irá aumentando.
La función que nos indica el capital es 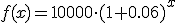 ¿Qué ocurrirá cuando x tienda a infinito?
¿Qué ocurrirá cuando x tienda a infinito?
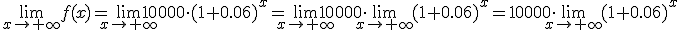
En la tabla siguiente puedes apreciar el valor del límite indicado.
| POTENCIAS |
|
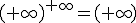 |
Si l > 1, |
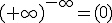 |
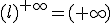 |
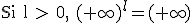 |
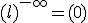 |
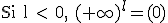 |
Si 0<l<1, |
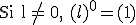 |
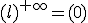 |
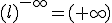 |
|
Halla el siguiente límite 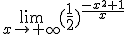
Calcula 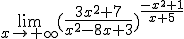
|
0
| |
|
1
| |
|
2
| |
|
-1
|
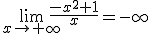 , entonces
, entonces