3.3. Plaga de conejos
 |
| Arctic Hare.Imagen obtenida de la Fundación Wikipedia bajo licenciaCreative Commons. |
La imagen que nos ha llegado de los conejos es siempre simpática y alegre. Desde el conejo que siempre llega tarde de Alicia en el Pais de las Maravillas, al conejo de Warner Bross, Bugs Bunny. Pero la realidad en muchas poblaciones es otra y se detectan plagas de conejos que eliminan cosechas completas. Si los conejos no tuvieran predadores ¿a qué cantidad llegarían?
Ya hemos visto varias situaciones donde se obtienen infinitos conejos, infinitas zanahorias, pero ... ¿son iguales todos los infinitos?
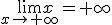 y que
y que 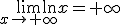 , pero ¿qué ocurriría con la función f(x) = x - ln(x)?
, pero ¿qué ocurriría con la función f(x) = x - ln(x)?| x | f(x)= x - ln(x) |
| 1 | 1 |
| 10 | 7,7 |
| 100 | 95,4 |
| 1000 | 993,1 |
| 10000 | 9990.8 |
| 100000 | 99988,5 |
Veamos una tabla para comprobar a donde tiende la función
Es decir, nos encontramos que el primer infinito es "mayor" que el segundo, por lo tanto, el límite de la función será infinito.
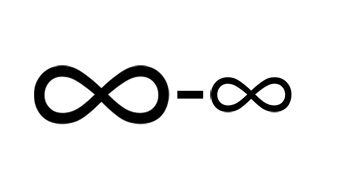
Así mismo, podriamos trabajar con la función f(x) = ln(x) - x. En este caso, también tenemos que el 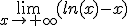 coincidirá con
coincidirá con 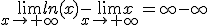 . Pero ahora el primer infinito es de orden inferior al segundo, por lo que estariamos ante la siguiente situación
. Pero ahora el primer infinito es de orden inferior al segundo, por lo que estariamos ante la siguiente situación
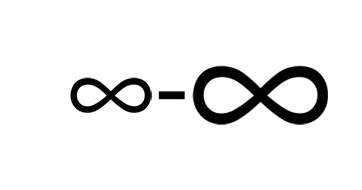
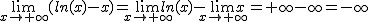 .
.
Ordenes de infinitos
Dadas dos potencias de x, la de mayor exponente es un infinito de orden superior.
Dadas dos funciones exponenciales de base mayor que 1, la de mayor base es un infinito de orden superior.
Cualquier función exponencial de base mayor que 1 es un infinito de orden superior a cualquier potencia de x.
Las potencias de x son infinitos de orden superior a las funciones logarítmicas.
Dos polinomios del mismo grado o dos exponenciales de la misma base son infinitos del mismo orden.
Indica el límite, cuando 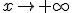 de las siguintes expresiones.
de las siguintes expresiones.
1. 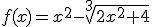
2. 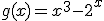
Ahora bien, podemos encontrarnos con funciones que no sean polinomios ó funciones radicales. En ocasiones, deberemos calcular límites donde aparezcan fracciones algebraicas, como en el caso siguiente:
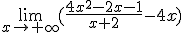
Aqui nos encontramos con dos infinitos pero no sabemos cuál es mayor. Para determinar el límite de la función, debemos realizar las operaciones algebraicas correspondientes para poder determinar el límite. Veamos este caso
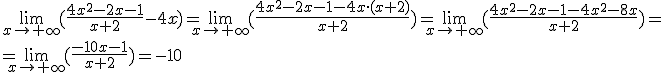
Calcula el límite de la siguiente función 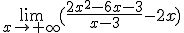
|
0
| |
|
-3
| |
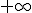
| |
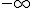
|
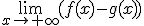 , debemos multiplicar y dividir por
, debemos multiplicar y dividir por 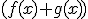 , para que desaparezcan las diferencias de raices. Veamos un ejemplo.
, para que desaparezcan las diferencias de raices. Veamos un ejemplo.
Calcula el siguiente límite 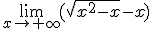
Determina el siguiente límite 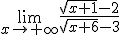
|
0
| |
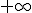
| |
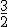
| |
|
1
|
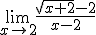
Em el apartado 3, cuando hablamos de las indeterminaciones, incluimos una serie de indeterminaciones de tipo potencial y exponencial, en concreto nos referimos a las del tipo 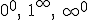 .
.
Esas indeterminaciones no vamos a tratarlas aquí pero si quieres conocer en qué consisten y como resolverlas puedes encontrar ejemplos resueltos en la siguiente dirección:
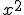 tiene grado dos y
tiene grado dos y 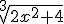 tiene grado
tiene grado 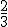 (lo obtenemos de convertir
(lo obtenemos de convertir 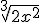 a
a 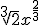 . Al ser mayor el primer grado, podemos decir que el límite de la función es
. Al ser mayor el primer grado, podemos decir que el límite de la función es 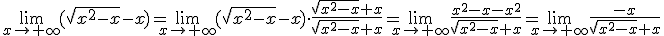
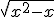 tiene un comportamiento igual al de la función g(x) = x , por lo que estamos ante un límite análogo a
tiene un comportamiento igual al de la función g(x) = x , por lo que estamos ante un límite análogo a 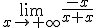 , por lo que el límite es igual a
, por lo que el límite es igual a 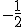
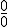 , para resolverla multiplicamos numerador y denominador por el conjugado del numerador.
, para resolverla multiplicamos numerador y denominador por el conjugado del numerador.