1.4. Cuando la cosa no tiene fin
 |
Hay veces que se pueden o deben tener controlados aspectos cotidianos. Nuestro peso, el número de personas en lista de espera para una operación, o los gastos de electricidad de nuestra casa. Pero otras veces hay cosas que se desbordan y no hay forma de contenerlas como el exceso de comidas cuando nos encontramos en Navidad, las obras en la ciudad cuando se acercan elecciones municipales o el número que se adscriben a la página de Facebook de un programa de éxito. En este apartado vamos a hablar de esos casos en que una función no se puede controlar.
En el applet siguiente tienes representada la función 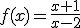 . Ve cambiando los valores de la variable x y observa hacia que valores tiende la función cuando la variable x tiende a 2 por la izquierda y por la derecha.
. Ve cambiando los valores de la variable x y observa hacia que valores tiende la función cuando la variable x tiende a 2 por la izquierda y por la derecha.
Escena de Descartes creada por Ángela Nuñez Castain bajo licencia Creative Commons.
Diremos que la función f(x) tiende a infinito cuando la variable tiende hacia un valor a, cuando el valor de la función se hace cada vez más grande o más pequeño a medida que nos acercamos al valor a. Se escribe como
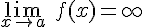
Como es evidente la función tiende a 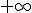 o
o 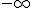 según las situaciones. Por ejemplo, en la función anterior tendríamos
según las situaciones. Por ejemplo, en la función anterior tendríamos
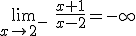
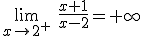
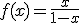 cuando x tiende a 1.
cuando x tiende a 1.
Hemos visto que ocurre en el caso en que la función se hace infinito cuando la variable se acerca a un valor, ¿pero qué pasa si es la variable la que tiende a infinito? Por supuesto puede darse el caso de que la función tambien se haga infinito. Por ejemplo , la función 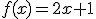 es evidente que mientras más grande se haga x más se hara la función y mientras más pequeña x más pequeña f(x). Sin embargo hay veces que no ocurre eso. Observa el siguiente applet donde aparece en amarillo representada la función
es evidente que mientras más grande se haga x más se hara la función y mientras más pequeña x más pequeña f(x). Sin embargo hay veces que no ocurre eso. Observa el siguiente applet donde aparece en amarillo representada la función 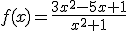 y fíjate hacia qué valores tiende la función cuando la x tiende a
y fíjate hacia qué valores tiende la función cuando la x tiende a 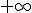 y
y 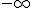 .
.
Modificación del applet de Descartes crado por José Luís Alonso Borrego, bajo licencia Creative Commons.
Si a medida que el valor de la variables se hace muy grande o muy pequeño la función tambien se hace cada vez más pequeña o más grande diremos que
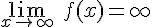
Si mientras más grande o más pequeña se hace la variable la función tiende a estabilizarse en un valor fijo b diremos entonces que
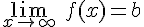
Evidentemente habrá que estudiar cuando la variable tiende a 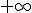 y a
y a 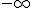 , pues puede darse el caso de que en ambos sentidos no tome el mismo valor.
, pues puede darse el caso de que en ambos sentidos no tome el mismo valor.
Eso no ocurre en el caso de la función del applet anterior, pues en este caso
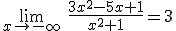
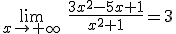
Toma la función del ejercicio resuelto anterior, haz una tabla de valores en los que des valores muy grandes y muy pequeños a la variable y responde el valor de los siguientes límites.
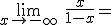
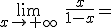
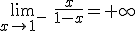 . Por la derecha cada vez se hace más grande en valor absoluto y por tanto se hace cada vez más pequeña la función y
. Por la derecha cada vez se hace más grande en valor absoluto y por tanto se hace cada vez más pequeña la función y 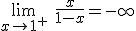 .
.