1.2. Depende del lado
 |
En general es corriente que tengamos que desplazarnos dentro de nuestra ciudad para ir de compras, al trabajo, a recoger a los niños al colegio, a ver algún amigo o familiar, etc. Esos desplazamientos pueden hacerse de distinta forma: andando, en coche propio, en autobús, en metro, en tranvía o en cualquier otro medio que nos ofrezca nuestra ciudad y que nos enlace con nuestro destino.
En los límites pasa algo parecido. Si te has fijado en los applets que hemos visto en el apartado anterior nosotros nos hemos podido acercar por la izquierda o derecha del punto. Incluso en las tablas de valores que usamos en el ejercicio resuelto anterior, verías que en un lado íbamos dando valores cercanos al 2 pero siempre menores y por el otro eran valores mayores acercándonos siempre al 2. Esto nos va a servir para definir los límites laterales.
Importante
Llamaremos límite por la derecha de la función f(x) al valor que se obtiene en la función cuando x se acerca al valor a por la derecha, es decir siempre por valores mayores que a. Se representa por
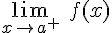
Hablaremos del límite de la función f(x) cuando x tiende al valor a por la izquierda a lo que se obtiene cuando a x le vamos dando valores cercanos al valor a por la izquierda, es decir, manteniéndose siempre por valores más pequeños. Se representa por
Ejemplo o ejercicio resuelto
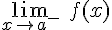
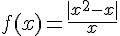, donde | | representa el valor absoluto de la expresión que hay dentro.
.
.
Importante
La condición para que exista el límite de una función en un punto es que existan los dos límites laterales y que coincidan. Si los límites laterales no coinciden entonces no existe el límite de la función en el punto. Se tiene por tanto:
AV - Actividad de Espacios en Blanco
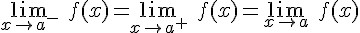
Consideremos la función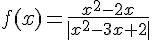 
, calcula los límites siguientes.
=
=
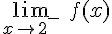
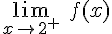
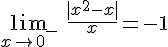