2. Te alcanzo en el infinito
 |
Quizás alguna vez al pasear por el campo o en alguna estación de tren pequeña te has colocado entre las vías del tren y has mirado a lo lejos. Seguro que te ha dado la sensación visual de que los dos railes de la vía se van acercando poco a poco y al final se juntan, aunque sabes perfectamente que eso no es posible porque los railes son paralelos. De todos modos los matemáticos suelen decir que dos rectas son paralelas cuando coinciden en el infinito. Pero hay más situaciones en las que perspectiva nos juega esta pasada. Si has estado en la playa y miras la línea del horizonte parece que el cielo y el mar se unen allí a lo lejos. En este apartado vamos a hablar de esos elementos que se unen en el infinito.
Se llaman asíntotas de una función a unas rectas con las que la función coincide en el infinito. Las hay de diversos tipos: verticales, horizontales y oblicuas.
Dada la función f(x) diremos que la recta de ecuación x=a es una asíntota vertical si se verifica
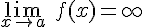
En el apartado anterior vimos un ejemplo de asíntota vertical en la función 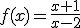 en donde vimos que si x se acercaba al valor 2 se tendía a infinito, con distinto signo según el lado. Por tanto x=2 es una asíntota vertical.
en donde vimos que si x se acercaba al valor 2 se tendía a infinito, con distinto signo según el lado. Por tanto x=2 es una asíntota vertical.
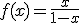 que vimos en el apartado anterior su asíntota vertical es x =
.
que vimos en el apartado anterior su asíntota vertical es x =
.
Diremos que la función f(x) tiene una asíntota horizontal y=b si la función tiende hacia b a medida que la variable tiende a infinito. Es decir, cuando se verifica
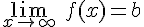
En el apartado anterior vimos que y=3 era una asíntota horizontal de la función 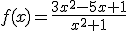 .
.
Una función si tiene asíntota horizontal sólo puede tener una, aunque puede no coincidir la misma cuando se tiende a 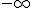 o a
o a 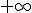 .
.
En el applet siguiente tiene representada una función racional 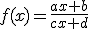 cuyos coeficientes puedes modificar con los deslizadores de la izquierda (siempre debe ser
cuyos coeficientes puedes modificar con los deslizadores de la izquierda (siempre debe ser 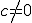 pues si no se convertiría en una recta). Puedes ver que posee dos asíntotas una vertical y otra horizontal.
pues si no se convertiría en una recta). Puedes ver que posee dos asíntotas una vertical y otra horizontal.
Lllamaremos asíntota oblicua de una función f(x) a una recta, de ecuación 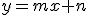 , con la que la función tiende a coincidir en el infinito.
, con la que la función tiende a coincidir en el infinito.
Para calcularla se utilizan las siguientes igualdades:
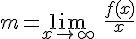
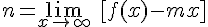
En la siguiente ventana tienes representada la función 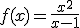 que, además de tener una asíntota vertical en x=1, tiene una asíntota oblicua en la recta y=x+1.
que, además de tener una asíntota vertical en x=1, tiene una asíntota oblicua en la recta y=x+1.
Si mueves el deslizador verde podrás ver como los puntos P sobre la función y Q sobre la asíntota cada vez se acercan más.
Con las asíntotas oblicuas pasa como con las horizontales. Si existen, sólo puede haber una, aunque puede ser distintas en 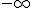 y
y 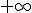 .
.
Pueden existir funciones que no tengan ningún tipo de asíntotas. Por ejemplo, la funciones polínomicas, sean del grado que sean, no tienen ninguna asíntota, salvo las líneas oblicuas que coincidirían con la asíntota oblicua.
Cuando en el tema siguiente aprendamos a calcular límites podremos hallar las asíntotas de distintas funciones.