1.1. Cuando el valor está claro.

Alturas
Es innegable que la raza humana evoluciona. Hay aspectos que van cambiando en cada generación. Uno de los aspectos de los que se suele hablar a menudo es la estatura. Se dice que cada generación, en media, es más alta que la generación anterior. Indiscutiblemente hoy día podemos ver a jugadores de baloncesto como Pau Gasol, que sobrepasan ampliamente los dos metros, con una proliferación que no era corriente hace cincuenta años. Es de suponer que centímetro a centímetro la altura de las personas seguirá aumentando, aunque hay algunos valores límite que no creemos que se puedan alcanzar. Por ejemplo, será difícil ver personas que midan tres metros. En otras situaciones pasa lo mismo. El récord en la carrera de los 100 metros suele ser superado últimamente por el corredor jamaicano Usain Bolt. Ese récord suele bajar de vez en cuando , estando el récord olímpico actual en 9,69 segundos. Es evidente que debe haber una cantidad límite, de la que no bajará esa velocidad, pues no podremos ver a nadie corriendo los 100 metros en 2 segundos, por poner un ejemplo.
Icono IDevice Importante

Supongamos que tenemos una función f(x) y dos valores a y L. La idea intuitiva nos dice que el límite de la función f(x) es L cuando la variable x tiende al valor a si, a medida  que vamos dándole a x valores más cercanos al valor a, la función va tomando valores más cercanos al valor L.

 

La forma de expresarlo es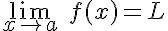


Para entender la idea tenemos el siguiente applet de Descartes. Ve modificando el valor de x, utilizando las flechas roja y azul, y comprueba en la pantalla como, a medida que x se va acercando al valor 1, la función se va acercando al valor 3. En este caso diríamos que .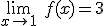

Modificación del applet creado por José Luís Alonso Borrego, bajo licencia Creative Commons.

Esta unidad interactiva requiere la máquina virtual de Java J2RE.
Icono de iDevice Ejemplo o ejercicio resuelto

Vamos a estudiar el límite de la función 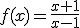cuando la variable x tiende a 2.

Para ello basta ir dándole valores a x que se vayan acercando a 2.


Puede ser que el valor a no pertenezca al dominio de la función, sin embargo si exista el límite de la función cuando x tiende a ese valor. Por ejemplo, si tenemos la función 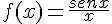, está claro que esa función no tiene sentido para x=0 porque se anula su denominador. Sin embargo si tiene límite. Comprueba con el siguiente applet que .

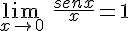Ve observando los valores que va tomando la función cuando x se va acercando a 0. Lo puedes ver en las coordenadas del punto P.

Applet de Descartes creado por Angela Nuñez Castain bajo licencia Creative Commons. 

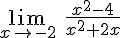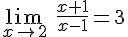Esta unidad interactiva requiere la máquina virtual de Java J2RE.
Ahora prueba tú. Construye una tabla de valores para saber cuál sería el valor del límite siguiente y responde a la pregunta.
Icono de iDevice AV - Actividad de Espacios en Blanco
Calcula el valor del siguiente límite.

= .

 

  

Icono IDevice Importante
En general, a la hora de calcular el límite de una función en un punto, es suficiente con sustituir el valor en la función. Si obtenemos un valor real, ése es el límite de la función. Si obtenemos algún valor indeterminado o infinito entonces hay que trabajar de distinta manera. En el tema siguiente veremos el cálculo de límites de una manera más rigurosa.

« Anterior | Siguiente »