2.3. Vacunando el plano
|
|
El Burj Khalifa es un rascacielos que se encuentra situado en el distrito Downtown Burj Khalifa de la ciudad de Dubái, en Emiratos Árabes Unidos. Es la estructura más alta construida por el hombre. La construcción comenzó el 21 de septiembre de 2004, y su inauguración oficial fue el 4 de enero de 2010.
Se localiza en la parte central de las costas de Dubái.Para verlo en Google Maps pulsa Aquí.
La fecha original de apertura del edificio iba a ser el 31 de diciembre del 2008, aunque, debido a un retraso en la construcción, su finalización e inauguración se vio retrasada hasta el 4 de enero de 2010.
Para realizar la animación que has visto en el vídeo anterior se ha utilizado un dibujo-maqueta que se ha trazado en un ordenador. Como base de la maqueta se ha utilizado un plano que pasa por tres puntos del espacio A=(3,0,0), B=(2,1,1) y C=(-2,4,2). Sobre dicho plano se ha levantado el edificio utilizando como eje la recta que pasa por el punto P=(5,2,8). Calcula la ecuación de esa recta y el punto del plano que coincide con el centro del suelo del edificio.
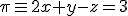 y es perpendicular a la recta
y es perpendicular a la recta 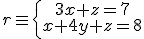
|
|
Cuando un rayo (recta) incide de forma perpendicular en un plano en el que rebota, este lo hace siguiendo la misma dirección pero en sentido contrario. Por ejemplo, si lanzamos un rayo de luz de forma perpendicular contra un espejo, el rayo rebota saliendo de forma perpendicular. Sin embargo, si en lugar de lanzarlo contra un plano, el rayo lo lanzamos contra una superficie no plana, rebota saliendo en una dirección con un ángulo distinto. Tal es el caso del vídeo que observas a la derecha en el que los rayos que llegan del Sol y rebotan en la chapa se concentran en un determinado punto concentrando todo el calor.
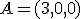 y dos vectores directores, en nuestro caso
y dos vectores directores, en nuestro caso 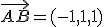 y
y 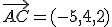 . Si el plano que buscamos tiene la forma
. Si el plano que buscamos tiene la forma
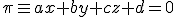 , su vector normal
, su vector normal 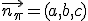 es perpendicular a los vectores directores, por tanto:
es perpendicular a los vectores directores, por tanto:
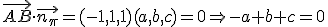
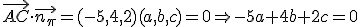
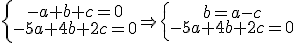
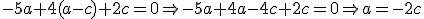
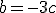 . Haciendo
. Haciendo 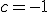 tenemos que:
tenemos que:
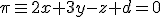 Puesto que el punto
Puesto que el punto 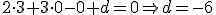 Luego la ecuación del plano es:
Luego la ecuación del plano es:
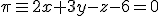
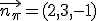 . De esta forma, tenemos que la ecuación de la recta es:
. De esta forma, tenemos que la ecuación de la recta es:
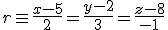
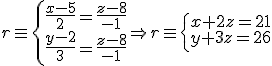
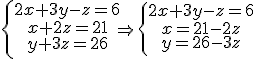 sustituyendo en la primera ecuación
sustituyendo en la primera ecuación
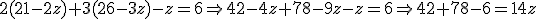
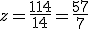 Luego
Luego
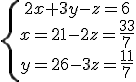
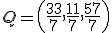
 , sus vectores directores deben ser perpendiculares. Como es paralela al plano
, sus vectores directores deben ser perpendiculares. Como es paralela al plano 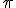 , el vector normal del plano y el vector director de la recta que buscamos son perpendiculares. Con las dos condiciones anteriores podemos calcular un vector director de la recta.
, el vector normal del plano y el vector director de la recta que buscamos son perpendiculares. Con las dos condiciones anteriores podemos calcular un vector director de la recta.