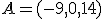2.2. Cayendo al vacío
|
|
Nos vamos a ocupar ahora del caso particular en el que nos encontramos con rectas o planos perpendiculares. en este caso, el ángulo que forman los dos elementos es de 90º. El coseno de 90º es 0, por lo que las operaciones se simplifican enormemente.
 |
En alguno de los ejercicios de apartados anteriores has observado que existen infinitas rectas que forman un ángulo de 60º con un plano o puedes comprobar que existen infinitos planos que forman un ángulo de 60º con otro plano. En la imagen de la derecha puedes observar que existen infinitos planos perpendiculares a otro dado y que pasen por un determinado punto pero, dada una recta, ¿Cuántas rectas perpendiculares a ella y que pasen por un punto existen? o dado un plano, ¿Cuántos planos perpendiculares a dicho plano y que pasen por dos puntos determinados existen?
Bueno, vamos a despejar algunas de estas dudas. Para empezar, en la siguiente pantalla interactiva puedes ver como si dos planos son perpendiculares, sus vectores normales también lo son.
- Arrastre el ratón para rotar la figura.
- Tecla S + movimiento vertical del mouse = zoom
- Una rejilla del PlanoXY se obtiene con Shift + G (de igual manera de deshabilita)
- Para ver con calidad mejorada, usar Shift +S (de igual manera de deshabilita)
 |
| CAD. Imagen obtenida de Flickr |
Un diseñador gráfico ha ideado la máquina que observas en la imagen de la derecha. Esta imagen va a ser utilizada en una película en 3D. Por este motivo, los programadores informáticos necesitan llevar el modelo gráfico a un modelo matemático con el que poder trabajar posteriormente para dotarlo de movimiento. En la pala que aparece a la derecha del diseño han observado que, debido a la regularidad de sus paredes, la pueden adaptar a dos planos perpendiculares. El primero de los planos lo han determinado, adaptándose a la ecuación 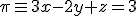 . Del segundo plano, dado que tiene que coincidir con otra pieza, saben que debe pasar por los puntos P=(2,-5,4) y Q=(-1,-3,6). Puedes ayudarles a determinar el segundo de los planos.
. Del segundo plano, dado que tiene que coincidir con otra pieza, saben que debe pasar por los puntos P=(2,-5,4) y Q=(-1,-3,6). Puedes ayudarles a determinar el segundo de los planos.
- Arrastre el ratón para rotar la figura.
- Arrastre los puntos rojos con el ratón.
- Shift + arrastre vertical = zoom
 , recta que pasa por el punto
, recta que pasa por el punto 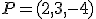 y que tiene como vector director
y que tiene como vector director 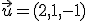 . Calcula la recta
. Calcula la recta  , que la corte perpendicularmente y que pase por el punto Q=(-2,5,1)
, que la corte perpendicularmente y que pase por el punto Q=(-2,5,1)
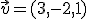
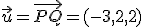 Luego la ecuación del plano sería:
Luego la ecuación del plano sería:
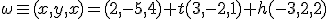
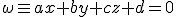 , dado que es perpendicular al plano
, dado que es perpendicular al plano 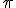 , entonces, sus vectores normales forman un ángulo de 90º, es decir:
, entonces, sus vectores normales forman un ángulo de 90º, es decir:
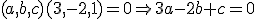
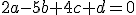
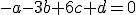
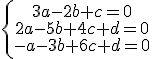 Despejamos y calculamos:
Despejamos y calculamos:
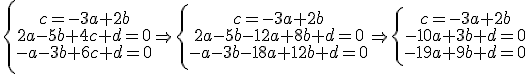
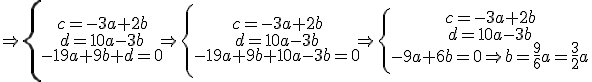
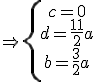 haciendo
haciendo 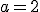
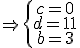
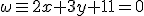
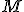 de la recta
de la recta 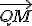 y le imponemos que sea perpendicular al vector
y le imponemos que sea perpendicular al vector 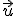 .
.
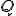 y tiene como vector director el vector
y tiene como vector director el vector 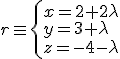
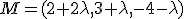
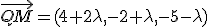 Ahora debemos imponer que sea perpendicular al vector
Ahora debemos imponer que sea perpendicular al vector 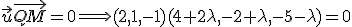 Es decir:
Es decir:
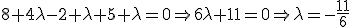
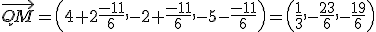
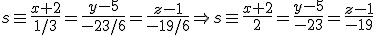
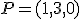 y tiene como vector director el vector
y tiene como vector director el vector 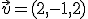 . La recta
. La recta  , perpendicular a
, perpendicular a 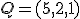 también pasa por el punto:
también pasa por el punto: