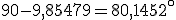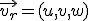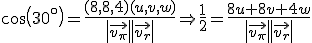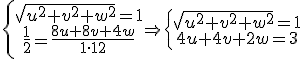2.1. Clavando una punta
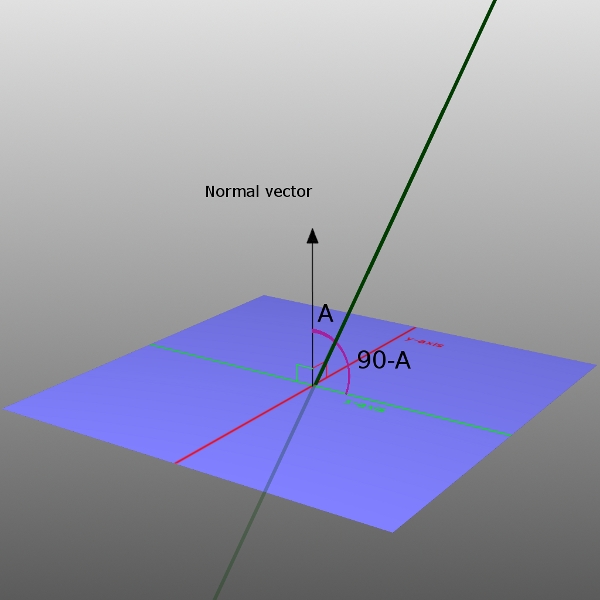 |
Hasta ahora hemos trabajado con el ángulo que forman dos rectas y el que forman dos planos pero ¿qué ocurre si tenemos una recta y un plano? Pues que también van a formar un ángulo. En la imagen de la derecha observamos el ángulo que forma la recta con el vector normal del plano (ángulo que forma el vector director de la recta con el vector normal del plano). Hemos llamado A a este ángulo. Pues bien, según observamos en esa imagen, el ángulo que forma la recta con el plano es 90-A.
Así, para calcular el ángulo que forma una recta con un plano calculamos primero el ángulo que forma el vector normal del plano con el vector director de la recta (ángulo menor de 90º). El ángulo que forma la recta con el plano resulta de restarle a 90º el ángulo anterior.
En la animación inferior observamos un caso extremo en el que el vector director de la recta es perpendicular al vector normal del plano. En este caso, el ángulo que forma la recta con el plano es 90º-90º=0º.
- Arrastre el ratón para rotar la figura.
- Arrastre el punto P para mover la recta.
- Shift + arrastre vertical = zoom
 |
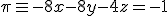 . Han observado que de este modelo, el filamento sigue la trayectoria de la recta
. Han observado que de este modelo, el filamento sigue la trayectoria de la recta
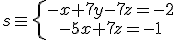
Según su estudio, deben insertar más filamentos de este tipo para mejorar el modelo, por lo que necesitan conocer el ángulo entre el filamento y la base del cepillo. Además, deben insertar un filamento en la base del cepillo que forme con éste un ángulo de 60º. Para ello quieren conocer algunas condiciones que debe cumplir la recta que contenga al filamento.
|
|
- Arrastre el ratón para rotar la figura.
- Tecla S + movimiento vertical del mouse = zoom
- Una rejilla del PlanoXY se obtiene con Shift + G (de igual manera de deshabilita)
- Para ver con calidad mejorada, usar Shift +S (de igual manera de deshabilita)
Dada la recta
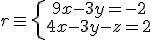 y el plano
y el plano 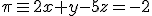
la recta y el plano forman un ángulo de
67,79º
| |
68,94º
| |
67,46º
| |
80,79º
| |
Dada la recta
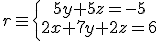 y el plano
y el plano 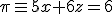
La recta y el plano forman un ángulo de
57,55º
| |
47,89º
| |
55,55º
| |
59,55º
| |
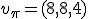 .
.
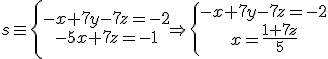
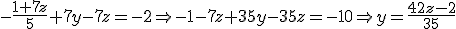
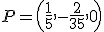
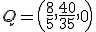
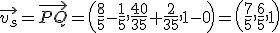 . Como ya sabes, el vector director de un recta no es único, sino que podemos tomar uno proporcional al anterior. En nuestro caso tomaremos
. Como ya sabes, el vector director de un recta no es único, sino que podemos tomar uno proporcional al anterior. En nuestro caso tomaremos
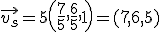
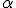 , entonces el ángulo que forman la recta y el plano es
, entonces el ángulo que forman la recta y el plano es 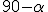 . Así:
. Así:
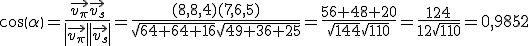
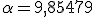 Luego el ángulo que forma el filamento con el cepillo es
Luego el ángulo que forma el filamento con el cepillo es