1.1. Posibles insignias en el ejército de las matrices
 |
Ahora vamos a estudiar una característica propia de las matrices que nos va a simplificar los cálculos y operaciones que debamos hacer utilizándolas.
Retomemos el caso de la cadena de supermercados que gestiona Raimundo. En este caso podríamos estar hablando de decenas de supermercados y de cientos de productos de los que llevar la gestión en esos supermercados. Por tanto, la matriz con la que llevaría Raimundo la gestión sería enorme. Si consiguiéramos quitar algunas filas o columnas de esa matriz, serían cálculos que estaríamos ahorrando ante el tratamiento matemático de esa matriz.
Veamos un ejemplo para que pueda ilustrar lo que estamos contando. Supongamos que la matriz de pedido de tres tipos de leche en cinco de los supermercados de los que lleva la gestión es la siguiente:

En este caso observamos que se ha realizado un pedido de 15 del tipo de leche 2 para el supermercado 4. Pero lo que a nosotros nos interesa es lo siguiente:
1.- El pedido de leche del supermercado 4 es el mismo que la suma de los pedidos de leche del supermercado 1, del supermercado 2 y del supermercado 3. Es decir:

2.- El pedido de leche del supermercado 5 es el mismo que el pedido del supermercado 1, menos la mitad del pedido del supermercado 2 mas el pedido del supermercado 3. Es decir:

De esta forma, si todos los cálculos que necesitemos realizar, en lugar de hacerlos con la matriz 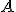 lo hacemos con la matriz que sólo tiene en cuenta los pedidos de leche de los supermercados 1, 2 y 3, es decir, la matriz
lo hacemos con la matriz que sólo tiene en cuenta los pedidos de leche de los supermercados 1, 2 y 3, es decir, la matriz

simplificaremos los cálculos enormemente. Posteriormente, para saber lo que ocurre con el supermercado 4 solamente deberemos utilizar la combinación lineal que se ha indicado en el anterior punto 1 y para saber lo que ocurre con el supermercado 5 solamente deberemos utilizar la combinación lineal que se ha indicado en el anterior punto 2.
En el caso anterior, las filas 4 y 5 son linealmente dependientes de las tres primeras, mientras que las tres primeras filas son linealmente independientes. En el caso anterior, podemos decir que el rango de 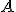 es 3 y lo expresaremos de la siguiente forma:
es 3 y lo expresaremos de la siguiente forma:

Además, es claro que  , por lo que observamos que, si a partir de una matriz cualquiera
, por lo que observamos que, si a partir de una matriz cualquiera  obtenemos otra matriz
obtenemos otra matriz  , añadiéndole a
, añadiéndole a  filas o columnas que sean linealmente dependientes con las que ya tiene la matriz
filas o columnas que sean linealmente dependientes con las que ya tiene la matriz  , el rango de las dos matrices es el mismo, es decir
, el rango de las dos matrices es el mismo, es decir 
 |
| Pescadería. Imagen obtenida del banco de imágenes del ITE. |
Así, se llama rango de una matriz A al número de filas (o columnas) linealmente independientes. Se representa por rg (A). En cualquier matriz el número de filas linealmente independientes coincide con el número de columnas linealmente independientes. El valor máximo que puede tener el rango de una matriz es el menor de los números correspondientes al número de filas y columnas.
De la definición anterior tenemos que el rango de una matriz a lo sumo
puede ser el número de filas o el número de columnas que tenga, el que
sea más pequeño de los dos. Así, si una matriz es de orden  , el rango de esa matriz a lo sumo puede ser 5, es decir, el rango podría ser 1, 2, 3, 4 ó 5.
, el rango de esa matriz a lo sumo puede ser 5, es decir, el rango podría ser 1, 2, 3, 4 ó 5.
Imagina en el caso de la gestión de la pescadería de los supermercados que lleva Raimundo, cómo podría ser de grande la matriz de pedidos del pescado para 15 supermercados. Inténtalo, solamente tienes que añadir a la matriz una columna por cada tipo de pescado que se venda... ¡¡Impresionante!!, por lo que quitando las filas y columnas que sean linealmente dependientes, simplificaríamos bastante los cálculos a realizar. De ahí la importancia de calcular el rango de una matriz y de obtener las filas y columnas que sean linealmente independientes.
En los siguientes puntos veremos dos formas de calcular el rango de una matriz. Ya verás que los dos son bastante sencillos.
Selecciona en cada caso la opción u opciones que consideres correctas.
Si  el rango de la matriz es
el rango de la matriz es
1
| |
2
| |
3
| |

| |

| |

| |
Si  observamos que
observamos que  . Entonces se dice que:
. Entonces se dice que:
 y y  son linealmente independientes son linealmente independientes
| |
 y y  son linealmente dependientes son linealmente dependientes
| |
 y y  no son proporcionales no son proporcionales
| |
Dada la matriz  si le añadimos la fila
si le añadimos la fila  obteniendo la matriz
obteniendo la matriz

En este caso tenemos que  es mayor que es mayor que 
| |
En este caso tenemos que  es menor que es menor que 
| |
Para calcular el rango de la matriz 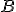 bastaría con calcular el rango de la matriz bastaría con calcular el rango de la matriz 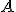
| |
En este caso tenemos que el rango de la matriz  puede que sea el mismo que el rango de la matriz puede que sea el mismo que el rango de la matriz 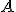
| |
En este caso tenemos que 
| |
En este caso tenemos que 
| |
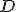 de orden
de orden  , selecciona la opción o las opciones que consideres correctas:
, selecciona la opción o las opciones que consideres correctas:
El rango de la matriz 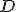 podría ser 2 podría ser 2
| |
El rango de la matriz 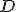 a lo sumo podría ser 6 a lo sumo podría ser 6
| |
El rango de la matriz 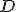 es 3 es 3
| |
El rango de la matriz 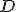 podría ser 1 podría ser 1
| |