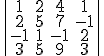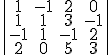Lo último que has visto en el apartado anterior es como, haciendo varios ceros en una línea de un determinante, es más fácil desarrollar dicha estructura. En este último apartado lo que vamos a ver es una generalización del método anterior y que, debido a las operaciones que vamos a realizar, es conocido por Método de Gauss. Como podrás ver en los dos siguientes temas de la Unidad, este método se puede utilizar en muchas ocasiones para resolver distintos problemas, hasta para hallar la solución de un sistema de ecuaciones.

El método de Gauss para hallar un determinante de cualquier orden, es una generalización del método que vimos al final del apartado anterior para desarrollar un determinante por una línea en la que se han hecho previamente ceros todos los elementos de una línea menos uno, que es por el que se desarrolla.

 

El objetivo del método es conseguir triangularizar la matriz que está dentro del determinante pues, de esa forma, es muy fácil hallar su valor, pues el determinante de una matriz cuadrada triangular (da igual que sea superior o inferior) es igual al producto de los elementos de la diagonal principal.

 

Las operaciones que podemos realizar con las líneas del determinante son:

1) Cambiar entre sí dos líneas. En ese caso el determinante cambia de signo, por lo que el determinante resultante debemos multiplicarlo por -1.

2) Multiplicar o dividir una línea por un número, pero en ese caso debemos hacer la operación contraria en el determinante, para que no cambie su valor.

3) Sumarle a una fila o columna otra paralela multiplicada por cualquier número. En este caso el valor del determinante no varía.

4) Lo usual es hacer ceros todos los elementos por debajo de la diagonal principal, utilizando, escalonadamente, los elementos de la diagonal principal, y por tanto su fila, para hacer ceros los que están debajo.

Veamos un ejemplo resuelto.